Bordeaux, juin 2003
| Extremum d’une fonction de deux variables sous contrainte linéaire |
| Équipe académique Mathématiques Bordeaux, juin 2003 |
Remarque
Document à destination des enseignants désirant construire un imagiciel présentant des surfaces et leurs sections par des plans parallèles aux plans de bases en Première ES ou Terminale ES et S.
Prérequis
Utilisation de Géospace et/ou des contrôles ActiveX.
Objectifs
Cette fiche montre, à partir d’un exemple, comment construire pas à pas la représentation graphique d’une fonction de 2 variables, ses sections par des plans parallèles aux plans de base ainsi que la visualisation de contraintes linéaires.
Ce canevas pourra être ensuite réutilisé pour créer d’autres imagiciels du même type
Description
Cette fiche utilise la nouvelle version de Géospace. Les constructions seront réalisées à partir d’un imagiciel de base contenant déjà des plans mobiles parallèles aux plans de base ainsi qu’un outil pour construire un plan d’équation y = a x + b
Cet imagiciel est disponible au choix :
- soit dans le fichier Geospace : Contrainte.g3w
- soit sous forme de contrôles Activex insérés dans une page traitement de texte (Lotus WordPro, Word 97, 2000 ou Xp), dans un classeur tableur (Excel 97, 2000 ou Xp) ou dans une page Web visualisée à l’aide d’Internet Explorer. Les fichiers disponibles sont (selon le cas) :
Contrainte LotusWordPro.lwp
Contrainte Word97.doc, Contrainte Word2000-Xp.doc
Contrainte Excel97.xls, Contrainte Excel2000-Xp.xls
Contrainte.htm
Il est nécessaire pour utiliser l’un de ces fichiers d’avoir au préalable installé les contrôles ActiveX du Creem sur la machine.
Construction de l’imagiciel
On se propose de réaliser un imagiciel montrant la représentation graphique d’une fonction de deux variables puis de visualiser les sections de cette surface par des plans parallèles aux plans de base ainsi que par des plans d’équation y = a x + b.
L’imagiciel sera construit à partir d’un fichier, disponible en téléchargement, contenant déjà les plans parallèles aux plans de base ainsi que les plans d’équation y = a x + b. Ce fichier peut être un fichier Géospace (nouvelle version), un fichier texte ou une feuille de calcul utilisant les contrôles ActiveX.
Commandes disponibles dans ce fichier
La touche 0 (zéro) permet de placer les 3 plans sur les plans de base.
La touche U permet de modifier au clavier (flèches) la taille des trois plans.
La touche H permet d'afficher le plan Ph.
La touche J permet d'afficher le repère orthonormé associé au plan Ph.
La touche Z permet de déplacer le plan Ph au clavier.
La touche F permet d'afficher le plan Pf.
La touche G permet d'afficher le repère orthonormé associé au plan Pf.
La touche X permet de déplacer le plan Pf au clavier.
La touche V permet d'afficher le plan Pv.
La touche B permet d'afficher le repère orthonormé associé au plan Pv.
La touche Y permet de déplacer le plan Pv au clavier.
La touche O permet d'afficher le plan Po d’équation y = a x + b .
La touche A permet de modifier la valeur de a au clavier.
La touche Q permet de modifier la valeur de b au clavier.
La touche 1 permet d'afficher l'intersection des plans Ph et Pv.
La touche 2 permet d'afficher l'intersection des plans Ph et Pf.
La touche 3 permet d'afficher l'intersection des plans Pf et Pv.
La touche 4 permet d'afficher l'intersection des plans Ph et Po.
Exemple proposé
Soit la fonction s définie par :
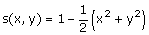 .
.
1. Construire la surface Cs d’équation :
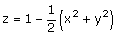
qui est la représentation graphique de la fonction s avec :
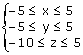 .
.
2. Examiner les courbes de niveau z = k de cette surface.
Caractériser ensuite ces courbes de niveau.
3. Déterminer l’équation de la courbe de niveau obtenue en coupant la surface par le plan d’équation y = 3 parallèle au plan xoz. On l’exprimera sous la forme z = g (x).
Expliquer pourquoi les courbes de niveau y = k sont des paraboles. Indiquer les coordonnées de leur sommet en fonction de k.
4. Déterminer l’équation de la courbe de niveau obtenue en coupant la surface par le plan d’équation x = 2. On l’exprimera sous la forme z = h (y).
Quelle est la nature des courbe de niveau x = k ? Préciser leurs éléments caractéristiques.
5. Recherche de l’extremum de la fonction s sous la contrainte y = 1 + x.
Dans l’espace quelle est l’interprétation graphique de l’équation de contrainte : y = 1 + x ?
Visualiser la surface et cette contrainte.
Déterminer l’extremum de la fonction s.
6. Faire un travail analogue sous la contrainte y = x – 3.
Représentation graphique de la surface
| Objets à construire Faire apparaître le repère par défaut. La fonction s définie par : afin de respecter la contrainte sur z ; le fait de diviser par permet de ne faire tracer Cs que lorsque : Sa représentation graphique Cs dans [-5 ; 5] x [-5 ; 5]. Créer une commande permettant d’afficher ou non cette surface. |
|
Courbes de niveau z = k
| Objets à construire Ces courbes de niveau sont les sections de la surface
Cs et du plan Ph parallèle au plan xoz et de d’équation
z = k. Pour construire la section de cette représentation graphique
avec le plan Ph il faut en connaître au préalable la nature :
dans le cas de cette fonction c’est le cercle lh centré sur l’axe
(oz) et de rayon : Créer une commande permettant de montrer ou de cacher cette section. Sur la figure ci-contre on trouve la courbe de niveau : z = - 6. |
|
| Visualisation d’une série de courbes de niveau z = k Cacher la surface Cs et placer le plan Ph de face. Appuyer sur la touche Z afin de pouvoir modifier la valeur de z au clavier. Modifier le pas de pilotage de z afin qu’il soit de 1 (Piloter / Modifier paramètres de pilotage au clavier). Sélectionner la section lh afin qu’elle laisse sa trace (Afficher / Sélection trace). Passer en mode Trace (Afficher / Mode Trace) et modifier z au clavier. Sur la figure ci-contre on trouve les courbes de niveau z avec z entier compris entre -10 et 0. |
|
Section par un plan parallèle au plan xoz : courbe de niveau y = 3
| Objets à construire Faire apparaître le plan Pv parallèle au plan xoz et d’équation y = k. Créer le point M (x ; y ; s(x,y)). Créer une commande permettant de montrer ou de cacher le point M. Ce point est dans le plan Pv, si on modifie x au clavier, il va se déplacer dans le plan. Créer la trace du point M en modifiant x. Créer le lieu lv du point M (le pilote sera x). Placer le plan Pv de face et modifier x au clavier. Créer une commande permettant d’afficher ou non le lieu lv du point M. |
|
|
|
Section par un plan parallèle au plan yoz : courbe de niveau x = 2
| Objets à construire Faire apparaître le plan Pf parallèle au plan yoz et d’équation x = k. Créer le point M (x ; y ; s(x,y)). Créer une commande permettant de montrer ou de cacher le point M. Ce point est dans le plan Pf, si on modifie y au clavier, il va se déplacer dans le plan. Créer la trace du point M en modifiant y Créer le lieu lf du point M (le pilote sera y). Placer le plan Pf de face et modifier y au clavier. Créer une commande permettant d’afficher ou non le lieu lf du point M. |
|
|
|
Extremum de la fonction s sous la contrainte y = 1 + x
| Objets à construire Faire apparaître le plan Po d’équation y = a x + b ;.affecter à a la valeur 1 et à b la valeur 1 (Piloter / Affecter une variable numérique libre). Créer le point N (x ; ax ; s(x ; ax + b)). Créer une commande permettant de montrer ou de cacher le point N. Ce point est dans le plan Po, si on modifie x au clavier, il va se déplacer dans le plan. Créer la trace du point N en modifiant x. Créer le lieu lo du point N (le pilote sera x). Placer le plan Po de face et modifier x au clavier. Créer une commande permettant d’afficher ou non le lieu lo du point N. |
|
|
|
Extremum de la fonction s sous la contrainte y = x - 3
| Objets à construire Créer le plan Pa d’équation y = x – 3 ainsi que sa représentation P5 (Créer / Objet selon prototype / Plan d’équation : y = a*x + b ; puis : Créer / Objet selon prototype / Visualisation du plan d’équation : y = a*x + b) ; rendre ensuite cette « image » opaque et demander à voir les parties cachées en pointillés. Créer une commande permettant de montrer ou de cacher P5. Créer le point N1 (x ; x-3 ; s(x ; x-3)) Créer une commande permettant de montrer ou de cacher le point N1. Ce point est dans le plan Pa, si on modifie x au clavier, il va se déplacer dans le plan. Créer la trace du point N1 en modifiant x. Créer le lieu la du point N1 (le pilote sera x). Placer le plan Pa de face et modifier x au clavier. Créer une commande permettant d’afficher ou non le lieu la du point N1. |
|
|
|