Bordeaux, juin 2003
| Du paraboloïde hyperbolique au cône |
| Équipe académique Mathématiques Bordeaux, juin 2003 |
Niveau
Terminale S – Enseignement de spécialité
Objectifs
D’une part : obtenir l’équation d’une hyperbole sous la
forme X² - Y² = Cste.
(On effectue un changement de repère dans la section du paraboloïde hyperbolique
par un plan parallèle au plan xoy. On justifie ainsi que les sections du cône
par des plans parallèles à son axe sont des hyperboles.)
D’autre part : justifier le nom de cette surface en étudiant ses sections par des plans parallèles aux plans de base d’un nouveau repère.
Organisation pratique
| On utilisera au choix : |
fichier : |
| >> l’imagiciel Geospace (il ne fonctionne qu’avec la nouvelle version de Geoplan-Geospace) |
hyper_cone.g3w |
| >> l’imagiciel intégré sous forme de contrôle ActiveX à ¤ une page traitement de texte (Lotus WordPro ou Word), ¤ un classeur Excel ou ¤ une page Html (visualisable uniquement à l’aide d’Internet Explorer) |
Hyper_cone_LotusWordPro.lwp Hyper_cone_Word97.doc Hyper_cone_Word2000-Xp.doc Hyper_cone_Excel97.xls Hyper_cone_Excel 2000-Xp.xls Hyper_cone_html.htm
|
Description
Séquence à utiliser en classe entière à l’aide d’un ordinateur couplé à un vidéo- projecteur.
L’enseignant utilise cet imagiciel dans le cadre de son cours pour mettre en évidence les sections du paraboloïde hyperbolique par des plans parallèles aux plans de base.
Il peut par ailleurs placer ces plans de face afin d’étudier plus précisément ces sections.
Il a aussi la possibilité de générer le paraboloïde hyperbolique à partir de l’une de ses sections par un plan parallèle aux plans de base.
Enfin, à partir du paraboloïde hyperbolique d’équation z = x . y
construit dans le repère par défaut, on effectue un changement de repère par
rotation d’axe oz et d’angle 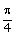 .
.
Partie 1 : Travail dans le repère par défaut
Les commandes de base
Cet imagiciel propose la visualisation du paraboloïde hyperbolique Cs d’équation : z = x . y.
On pourra visualiser ses sections par trois plans parallèles aux plans de base : Ph est le plan parallèle au plan xoy, Pf est le plan parallèle au plan yoz, Pv est le plan parallèle au plan zox
| La touche S permet d’afficher la surface Cs La touche H permet d’afficher le plan Ph et son intersection Lh avec la surface Cs ; le plan Ph peut alors être déplacé à l’aide des flèches de direction. |
|
| La touche J permet d’afficher le repère orthonormé associé au plan Ph. La touche Z permet de choisir à tout moment de déplacer à l’aide des flèches de direction le plan Ph. La touche F permet d’afficher le plan Pf et son intersection Lf avec la surface Cs ; le plan Pf peut alors être déplacé à l’aide des flèches de direction. |
|
| La touche G permet d’afficher le repère orthonormé associé au plan Pf. La touche X permet de choisir à tout moment de déplacer à l’aide des flèches de direction le plan Pf. |
Section par le plan Pf |
| La touche V permet d’afficher le plan Pv et son intersection Lv avec la surface Cs ; le plan Pv peut alors être déplacé à l’aide des flèches de direction. La touche B permet d’afficher le repère orthonormé associé au plan Pv. La touche Y permet de choisir à tout moment de déplacer à l’aide des flèches de direction le plan Pv. |
|
| La touche 0 (zéro) permet de replacer les trois plans sur les plans de base. La combinaison de touches CTRL+F1 permet à tout moment de retrouver la figure dans sa position de départ |
|
Pour aller plus loin : placer un plan de face
Afin d’étudier de manière plus précise les sections du paraboloïde hyperbolique par un plan parallèle aux plans de base, l’imagiciel offre la possibilité de placer ce plan de face.
| La touche E permet de placer le plan Ph de face (il est préférable d’avoir au préalable fait afficher ce plan). |
|
| La touche R permet de placer le plan Pf de face (il est préférable d’avoir au préalable fait afficher ce plan). |
Section par le plan Pf |
| La touche T permet de placer le plan Pv de face (il est préférable d’avoir au préalable fait afficher ce plan). |
|
| La combinaison de touches CTRL+F1 permet à tout moment de retrouver la figure dans sa position de départ |
|
Reconstruire la surface à partir de l’une de ses sections
Les commandes proposées vont permettre de reconstruire le paraboloïde hyperbolique à partir de l’une de ses sections ; ces commandes utilisent le mode Trace de Geospace qu’il faudra quitter avant toute nouvelle manipulation en appuyant sur la touche Echap.
Avant d’utiliser ces commandes on cachera au préalable la surface Cs en appuyant sur la touche S.
Remarque :
Pour améliorer la fluidité de l’affichage il est possible de modifier le pas de déplacement des objets mobiles (plans ou génératrice) à l’aide du menu : Piloter è Modifier les paramètres de pilotage.
| A partir de la section par le plan horizontal Ph — Appuyer sur la touche H pour faire afficher le plan Ph et la section Lh. — Appuyer sur la touche 7, puis sur les flèches de direction pour déplacer le plan Ph. |
|
| A partir de la section par le plan frontal Pf — Appuyer sur la touche F pour faire afficher le plan Pf et la section Lf. — Appuyer sur la touche 8, puis sur les flèches de direction pour déplacer le plan Pf. |
Avec le plan frontal Pf |
| A partir de la section par le plan vertical Pv — Appuyer sur la touche V pour faire afficher le plan Pv et la section Lv. — Appuyer sur la touche 9, puis sur les flèches de direction pour déplacer le plan Pv. |
Partie 2 : travail dans le nouveau repère
Étude théorique
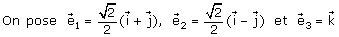
1. Montrer que le repère 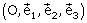 est un repère orthonormal.
est un repère orthonormal.
2. Déterminer l’équation de (Cs) dans ce nouveau repère et étudier les sections de (Cs) par les plans parallèles aux nouveaux plans de base.
3. Dans le cas de la section de (Cs) par le plan d’équation X = a, calculer les coordonnées du sommet Sa de la parabole et donner le lieu de Sa quand a décrit R.
4. Dans le cas de la section de (Cs) par le plan d’équation
Z = k, on sait que ce sera encore une hyperbole. On obtient alors
une autre équation de l’hyperbole : écrire la nouvelle équation de cette
hyperbole. on peut étudier cette courbe dans le plan pour vérification. Pour
k = 2, étudier la fonction 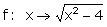 et construire sa représentation
graphique ; retrouver l’hyperbole par symétrie
et construire sa représentation
graphique ; retrouver l’hyperbole par symétrie
5. On peut chercher les équations des sections de (Cs) par les plans Pf ou Pv.
Étude expérimentale
Dans l’imagiciel le changement de repère s’effectue en appuyant sur la touche W ; l’affichage de la variable r permet de vérifier quel est le repère actif :
r = 1 si l’on travaille dans le repère par défaut Rxyz
r = 2 si l’on travaille
dans le repère ![]()
Toutes les commandes décrites dans la partie 1 sont opérationnelles et permettent d’effectuer au fur et à mesure des visualisations des résultats théoriques ; en voici ci-dessous quelques exemples.
| Intersection de Cs et du plan horizontal Ph |
|
| Dans le repère par défaut ou en vue de face |
Dans le repère
ou en vue de face |
| Intersection de Cs et du plan frontal Pf |
|
| Dans le repère par défaut |
Dans le repère
|
| Reconstruction de la surface Cs à partir de sa section par le plan frontal Pf |
|
| Dans le repère par défaut |
Dans le repère
|
Conclusion
Dès lors que l’élève sait qu’une équation du type X² + Y² = Cste est l’équation d’une hyperbole, on peut alors justifier que la section du cône par un plan parallèle à son axe est une hyperbole.