Projet d'activité TICE
Niveau :
Seconde
Objectif :
Conjecturer et démontrer.
Cadre d’utilisation
Séance 1
Les élèves travaillent sur le logiciel avec la fiche élève. Ils doivent faire la démonstration à l'issue de la séance (ou l’exercice est réalisé à la maison).
Séance 2
Correction de la démonstration par le professeur au vidéo projecteur ou au T.B.I.. Commandes : touches (Geoplan) ou curseur (GeoGebra)
d : affiche les angles droits
s : code les segments de même longueur OA et OB
a : code les angles de même mesure ![]()
b : code les angles de même mesure ![]()
t : fait apparaître les deux triangles isométriques
Travail à réaliser
1. Avec un logiciel de géométrie :
Construire le carré ABCD de centre O en prenant AB = 3.
M est un point libre sur le segment [AD].
Construire l'équerre OPQ en prenant OP = 4 et OQ = 5. Placer N.
Colorier le quadrilatère MONA.
Faire afficher l’aire du quadrilatère MONA.
Faire bouger le point M.
Quelle conjecture peut-on faire ?
2. Démonstration :
Quel rapport y-a-t-il entre l'aire du quadrilatère MONA et l'aire du carré ABCD ?
Démontrer ce résultat.
Problème :
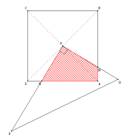
ABCD est un carré de centre O.
OPQ est une équerre qui pivote autour de O de manière que [OP] coupe [AD] en M et [OQ] coupe [AB] en N.
Que peut-on conjecturer pour l’aire du quadrilatère MONA lorsque l’équerre pivote autour de O ?
Fichiers disponibles