Optimisation dans l’espace |
|
Projet d'activité créé lors
d'un stage |
|
1ère ES option maths – Terminale S
Dans l'espace rapporté à un repère orthonormal
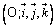on considère les points A(0;6;0), B(0;0;8) et C(10;0;8).
M est un point appartenant au segment [OB].
Le plan (P) passant par M et orthogonal à la droite (OB) coupe la droite (AC) en R.
On note respectivement N et S les points d'intersection du plan (P) avec les droites (OC) et (AB).
Le but de l'exercice est de déterminer quelle est la position du point M rendant maximale l'aire du quadrilatère MNRS.
Dans l'espace rapporté à un repère orthonormal
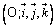on considère les points A(0;6;0), B(0;0;8) et C(10;0;8).
M est un point appartenant au segment [OB].
Le plan (P) passant par M et orthogonal à la droite (OB) coupe la droite (AC) en R.
On note respectivement N et S les points d'intersection du plan (P) avec les droites (OC) et (AB).
Le but de l'exercice est de déterminer quelle est la position du point M rendant maximale l'aire du quadrilatère MNRS.
A – CONJECTURE
1) Construire la figure à l'aide de Geospace.
2) Les points M, N,
R et S sont-ils coplanaires ?
Quelle semble être la nature du quadrilatère MNRS ?
3) Créer un affichage des coordonnées du point M et de l'aire du quadrilatère MNRS associé.
4) Conjecturer la position du point M pour laquelle l'aire du quadrilatère MNRS est maximale.
B – DÉMONSTRATION
1) Justifier la nature du quadrilatère MNRS.
2) Exprimer les coordonnées des points N, R et S en fonction de celles du point M.
3) Résoudre l'exercice.