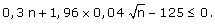A- Variables aléatoires discrètes.

I - Loi binomiale

   Champ d'application
Échantillonnage non exhaustif : tirages successifs avec remise.
Dans une population P, on étudie un caractère qualitatif C. Dans cette population :
- la proportion d'éléments possédant le caractère C est notée p.
- la proportion d'éléments ne le possédant pas est notée q. On a q = 1-p.
De cette population on extrait, au hasard, successivement, avec remise, des échantillons de n individus : il y a indépendance des tirages.
On définit ainsi la variable aléatoire X qui, à chaque échantillon de taille n, associe le nombre d'éléments possédant le caractère C.

   Loi de probabilité
.

   Caractéristiques

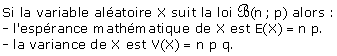
II. Loi hypergéométrique

   Champ d'application
Échantillonnage exhaustif : tirages successifs, sans remise, ou tirages simultanés.
Dans une population P de N individus, on étudie le caractère qualitatif C :
- a d'entre eux possèdent le caractère C.
- b ne le possèdent pas.
On a évidemment  a + b = N.
De cette population, on extrait au hasard, simultanément, ou successivement sans remise, des échantillons de n individus.
On définit ainsi la variable aléatoire X qui à chaque échantillon de taille n, associe le nombre d'éléments qui possèdent le même caractère C.

   Loi de probabilité
.

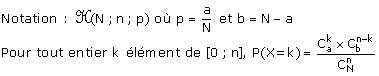   Caractéristiques

Théorème de convergence

Dans le cas de tirages d'échantillons de petite taille dans une population extrêmement nombreuse

Exercice

Pierre Carré et Alain Fini figurent parmi N candidats à l'oral d'un concours. Ils ont appris, par une indiscrétion, que sur les N questions que l'examinateur posera ce jour là, par tirage au sort, sans remise, a portent sur les statistiques. Or tous deux sont allergiques à cette spécialité.
Pierre Carré, après avoir naturellement fait le tour du problème, décide de passer l'épreuve en premier, tandis qu'Alain Fini, par nature attentiste, décide de passer le dernier… sûrs tous deux, d'avoir choisi la solution leur permettant d'avoir la plus grande probabilité d'éviter la question redoutée.
On précise de plus, que les conditions du concours sont telles, que le candidat ne peut savoir le type de question posé au candidat qui l'a précédé.

1. On considère l'ensemble composé des trois premiers candidats et on désigne par X la variable aléatoire qui prend pour valeurs le nombre de questions de statistiques posées. Déterminer la loi de probabilité de X, son espérance mathématique et sa variance.

2. Soit k un élément de [1, N] et E_k l'événement: « le candidat k tire une question de statistiques ».

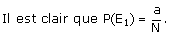
Déterminer P(E₂).
Quelle conjecture ce résultat suggère t- il ?

3. Pour démontrer cette conjecture, on se propose d'utiliser un dénombrement.

a. Les N questions posées par l'examinateur étant tirées au sort sans remise, constituent une permutation de N éléments.
Combien y a-t-il de telles permutations ?

b. Parmi celles-ci, dénombrer celles qui réalisent E_k. En déduire P(E_k).

B- Variables aléatoires continues

1. Loi normale

   Champs d’application
La loi normale intervient dans la modélisation des phénomènes aléatoires possédant de nombreuses causes indépendantes dont les effets s’ajoutent sans que l’un d’eux soit dominant. Elle tire son importance du fait que, sous certaines conditions, plusieurs autres lois convergent vers elle.

   Loi de probabilité

   Addition de variables aléatoires normales indépendantes
.
Ce théorème se généralise à l’addition de n variables aléatoires mutuellement indépendantes.

2. Loi normale centrée réduite

   Théorème fondamental

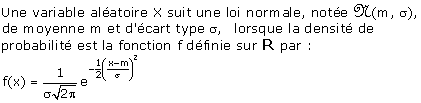
   Densité de probabilité
La densité de probabilité de la loi normale réduite centrée est la fonction f, définie sur R par :

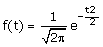
   Il existe des tables donnant les valeurs prises par la fonction de répartition, notée P, de la loi normale réduite centrée :

3. Usage des tables

Ces tables sont construites uniquement pour t positif mais les deux propriétés « graphiques » suivantes :

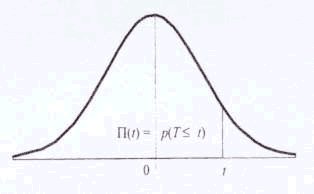
   La courbe est symétrique par rapport à l’axe des ordonnées

   L’aire de la surface comprise entre la courbe et l’axe des abscisses est égale à 1, permettent d’effectuer des calculs dans tous les cas.

Quelques résultats importants :

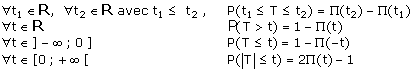
Cette dernière relation est fondamentale dans la suite de l’exposé et il est utile de retenir deux valeurs importantes :

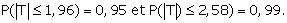
Plus simplement on pourra mémoriser le graphique suivant :

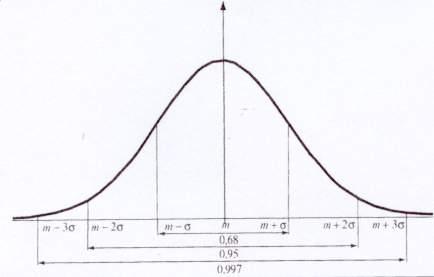
Exercice 1

On suppose que les notes obtenues à un concours par les 250 candidats, suivent une loi normale de moyenne m = 9,5 et d'écart type s = 2,1.

1. Combien de candidats ont obtenu une note supérieure ou égale à 10 ?

2. Le nombre de reçus étant 50, calculer la note du dernier reçu.(résultat arrondi au centième).

Exercice 2

Un laboratoire veut fabriquer des pilules se composant de deux substances A et B. Pour chaque pilule de la fabrication on considère les masses a et b respectivement des substances A et B qui la constituent.
On désigne par X la variable aléatoire qui, à chaque pilule tirée au hasard, associe la masse de la substance A et Y la variable aléatoire qui associe à chaque pilule la masse de la substance B.
On suppose que ces deux variables aléatoires sont indépendantes et suivent des lois normales de moyennes respectives : m_x = 8,55 mg. et m_y = 5,20 mg. et d'écarts types respectifs : .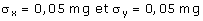

1. Déterminer à 10^-4 prés les probabilités : P(8,45 < X < 8,70) et P(5,07 < Y < 5,33).

2. On impose les normes de fabrication suivantes : 8,45 < a <8,70 et 5,07 < b < 5,33.
Calculer le pourcentage de pilules qui seront hors normes à la sortie de la chaîne.
Peut-on alors retenir ce procédé de fabrication, sachant que le pourcentage de pilules ne peut dépasser 1% ?

Exercice 3

Des machines fabriquent en série des plaques de tôle destinées au montage de transformateurs électriques. Ces plaques sont empilées et servent de conducteur au champ magnétique du transformateur. L'expérience montre que, lors de la fabrication, la probabilité qu'une plaque tirée au hasard soit inutilisable est 0,001.

Partie A

On désigne par Y la variable aléatoire qui, à chaque plaque utilisable, associe son épaisseur exprimée en millimètres.
On suppose que Y suit une loi normale de moyenne 0,3 mm. et d'écart type s.
Soit A l'événement : « Une plaque, tirée au hasard dans la production, a une épaisseur inférieure à 0,35 mm ».

1. On suppose  s = 0,04 mm. Calculer P(A) à 10^-2 prés.

2. On souhaite que P(A) = 0,95. Déterminer alors s.

Partie B

La réalisation d'un transformateur nécessite un empilage de n plaques prises au hasard et numérotées de 1 à n (n entier naturel non nul).
On désigne par Y_i la variable aléatoire prenant pour valeur l'épaisseur de la plaque numérotée i (1 £ i £ n).
Chacune des variables aléatoires Y_i suit la même loi que la variable Y définie dans la première question de la partie A.
Les n variables aléatoires Y_i  sont mutuellement indépendantes.
On appelle H_n la variable aléatoire prenant pour valeur la hauteur de l'empilage, c'est à dire H_n = Y₁ + Y₂ + …+ Y_n .

1. Calculer en fonction de n l'espérance mathématique et la variance de H_n.

2. On suppose que H_n suit une loi normale.

a. Montrer que la valeur maximale n₀  de n telle que p(H_n < 125) ³ 0,975 est solution de l'inéquation :

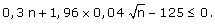
b. En posant 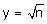 résoudre cette inéquation et en déduire n₀.

C. Approximation d’une loi par une autre
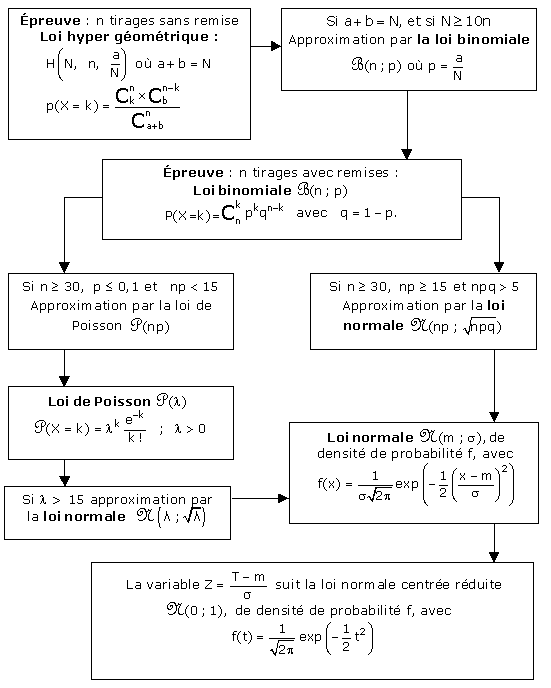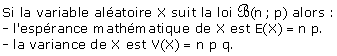
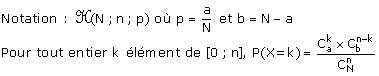
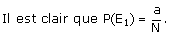
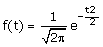
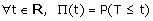
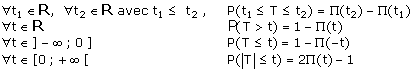
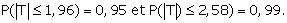
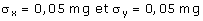