Dans ce chapitre, on s’intéresse à des séries statistiques discrètes ; de façon générale, on note x_i les valeurs prises par la série et n_i les effectifs correspondant à ces valeurs.

1. Représentation graphique

a) Le diagramme en bâtons permet de visualiser une distribution de fréquences mais aussi de repérer une distribution correspondant à un échantillon d’une loi connue (normale, uniforme, etc..)

b) Le regroupement en classes et l’histogramme permettent une illustration graphique d’un résultat , utile pour une série qualitative, plus discutable sinon en raison de la partialité du regroupement.

c) Le « camembert » est un bon moyen de visualiser une série avec peu de valeurs.

2. Caractéristiques de position

Mode

On appelle mode une valeur du caractère ayant le plus grand effectif ; dans le cas d’une répartition par classe, on parle de classe modale.

Moyenne

La moyenne d’une série statistique est définie par :

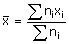
C’est donc la moyenne des valeurs prises pondérées par leurs effectifs.

Étant donné une série statistique(x₁ , x₂ , … , x_n), les x_i pouvant être égaux, on appelle dispersion des carrés des écarts autour de x le nombre e(x) défini par
 ;
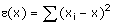e(x) est donc minimale pour 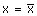C’est le réel le plus proche des x_i au sens des moindres carrés.

En effet, en développant l’expression de e(x), on obtient un trinôme du second degré de la forme :
 ;

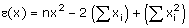 Médiane

Étant donné une série dont on a rangé les termes dans l’ordre croissant, on définit la médiane ainsi :

    - si le nombre de termes est impair, de la forme 2n + 1, la médiane de la série est le terme de rang n + 1 ;

    - si le nombre de termes est pair, de la forme 2n, la médiane de la série est la demi somme des valeurs des termes de rang n et n + 1.

Dans tous les cas, il y a au moins 50 % des termes de la série inférieurs ou égaux à la médiane, et au moins 50% des termes de la série supérieurs ou égaux à la médiane.

Étant donné un série statistique (x₁ , x₂ ,…..,x_n) , on appelle dispersion des écarts absolus autour de x le nombre e’(x) défini par :
.
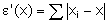e’(x) est minimum pour une valeur de x la plus proche des x_i au sens de l’écart absolu. La médiane est une valeur qui réalise ce minimum.

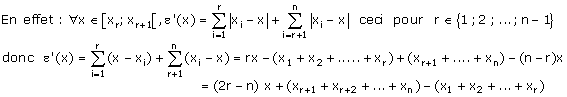
e’ est donc une fonction affine par morceaux, décroissante tant que r est inférieur à n / 2 et croissante quand r est supérieur à n / 2 ; plus précisément, on distingue 2 cas :

- si n est pair, n = 2n’, alors e’ est constante sur [x_n’ ; x_n’+1]

- si n est impair, n = 2n’ + 1, alors e’ est décroissante puis croissante avec un minimum pour x = x_n’+1 .

On retrouve bien la médiane dans les deux cas .

La question qui se pose ensuite est celle de la pertinence du choix de la moyenne ou de la médiane.

Pour une entreprise , de façon générale, le salaire moyen et le salaire médian sont très différents et la comparaison du salaire moyen et du salaire médian permet d’obtenir des renseignements sur la répartition des employés par catégories socio-professionnelles.
Dans un examen, c’est la moyenne qui va être utile, dans un concours, c’est la médiane(ou un quantile).
La moyenne est perturbée par des données aberrantes, pas la médiane. Pour éviter d’obtenir une moyenne ayant peu de sens, on calcule parfois une moyenne élaguée, c’est à dire une moyenne calculée après avoir enlevé des valeurs aberrantes à la série.
Par contre, on peut calculer une moyenne en faisant la moyenne des moyennes de sous groupes ce qui permet d’éviter les erreurs sur des grands nombres ; ceci est bien sûr inenvisageable pour la médiane.
De même, la moyenne a une propriété de linéarité, c’est à dire que :
.
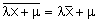C’est la version statistique de la propriété de l’espérance en probabilité.

Par contre, en général, la moyenne des carrés n’est pas égale au carré de la moyenne : leur différence est la variance.

Remarques

Il est peu intéressant de faire calculer des moyennes et des médianes aux élèves dans le cas d’une répartition des données en classes, puisque, à moins d’une répartition parfaitement régulière , ce ne sont pas la vraie moyenne ni la vraie médiane que l’on obtiendra ; par contre, il est sûrement intéressant de montrer aux élèves sur des exemples avec des répartitions très hétérogènes qu’on obtient des résultats qui peuvent être très éloignés des résultats théoriques.

Il existe d’autres moyennes que la moyenne arithmétique ; par exemple la moyenne géométrique (taux bancaire moyen) ou la moyenne harmonique (cours moyen d’une devise).

3. Caractéristiques de dispersion

Étendue

L’étendue d’une série est la différence entre la plus grande et la plus petite valeur.

Variance – Écart type

La variance d’une série statistique est le nombre défini par :
.

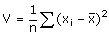C’est donc la moyenne des carrés des écarts à la moyenne.

C’est aussi la moyenne des carrés à laquelle on retranche le carré de la moyenne, soit
.

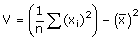En reprenant la fonction e du paragraphe précédent, on remarque que la variance est la valeur du minimum de , atteint pour .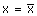
La variance étant une moyenne de carrés, elle n’est pas dans la même unité que les valeurs de la série ; on s’intéresse alors plutôt à la racine carrée de la variance, c’est l’écart type. 
Il caractérise la dispersion des valeurs autour de la valeur moyenne, on le note s.
On peut simplifier les calculs d’écart type grâce à la propriété suivante : s(lx + m) = |l| s(x).
De toute façon, les calculatrices donnent l’écart type sans problème.

4. Quantiles

Définition

Étant donné une série statistique, on définit la fonction quantile Q, de [0 ;1] dans l’ensemble des valeurs de la série, par : Q(u) = inf { x / F(x) ³ u}, où F(x) désigne la fréquence des éléments de la série inférieurs ou égaux à x.

Pour obtenir un quantile Q, on ordonne la série par ordre croissant, et si n est le nombre d’éléments de la série, Q(u) est la valeur du terme de cette série dont l’indice est le plus petit entier supérieur ou égal à nu.

Avec cette définition, les 3 quartiles sont Q(0,25), Q(0,5), Q(0,75) et on peut remarquer que cette définition ne donne pas le même résultat pour la médiane dans le cas où n est pair puisque Q(u) est toujours un élément de la série.

De façon générale, on s’intéresse aux quartiles Q(0,25) et Q(0,75) et à la médiane définie au § II.

On définit de même les 9 déciles qui sont les valeurs de Q(i/10) pour i = 1,2,….,9, et on s’intéresse surtout au premier et au neuvième décile.

Intervalle interquartile : intervalle dont les extrémités sont le premier et le troisième quartile. On a donc la moitié de l’effectif dans cet intervalle.

Intervalle interdécile : intervalle dont les extrémités sont le premier et le neuvième décile. On a donc 80% de l’effectif dans cet intervalle.

La longueur de ces intervalles est appelée écart, on a donc l’écart interquartile et l’écart interdécile.

5. Diagrammes en boîtes

Document du GEPS de mathématiques – 22/12/ 2000

Ces diagrammes sont aussi appelés diagrammes de Tuckey, diagrammes à pattes ou à moustaches (whiskers plot). Il n’y a pas que le nom qui varie d’un logiciel à l’autre. Les deux situations les plus classiques sont représentées ci-dessous :

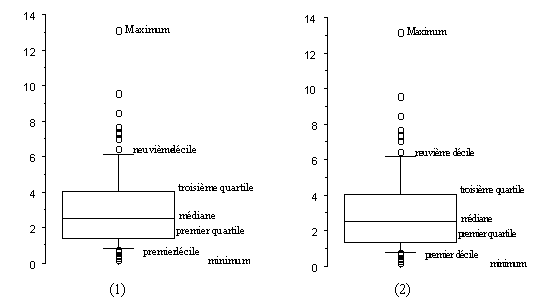
Nous conviendrons de choisir « par défaut »la définition représentée graphiquement en (1), où figurent les premiers et neuvièmes déciles. Si une ou plusieurs valeurs extrêmes sortent résolument des limites du dessin, on indique dessous leurs valeurs sans les représenter.

Néanmoins, les enseignants pourront utiliser des boites dont les extrémités sont les 1^er et 99^eme centiles, les valeurs extrêmes, etc. . L’essentiel est d’avoir compris le principe : un jour d’examen, on demandera simplement à l’élève de spécifier en légende les éléments représentés.

Les premiers diagrammes en boites sont les diagrammes de Tuckey où la longueur des « moustaches » est 1,5 fois l’écart inter-quartile ; les diagrammes de Tuckey étaient utilisés dans des secteurs où les données peuvent le plus souvent être modélisées en utilisant une loi de Gauss ; dans ce cas, au niveau théorique, les extrémités des « moustaches » sont voisines du premier et 99^ème centile : ces diagrammes étaient surtout utilisés pour détecter la présence de données exceptionnelles. On utilise aujourd’hui les diagrammes en boites pour représenter des distributions empiriques de données quelconques, non nécessairement symétriques autour de la moyenne, et le choix de moustaches de longueurs 1,5 fois l’écart interquartile ne se justifie plus.

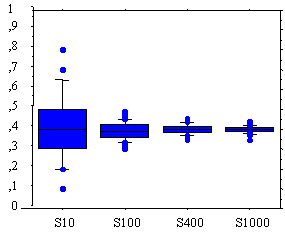
Les diagrammes en boites, comme les histogrammes, résument graphiquement une série ; l’idée de base est la suivante : au lieu de partager l’ensemble des valeurs possibles en segments égaux, on les partage en segments (quartile, déciles, centiles) qui contiennent une proportion prédéterminée des valeurs de la série. Les diagrammes en boîtes permettent de visualiser certains phénomènes et notamment de comparer plusieurs répartitions de valeurs. Ainsi, dans la figure ci-dessous, on a représenté les diagrammes en boîtes de :

– 100 simulations d’un sondage de taille 10 dans une population dont les individus sont codés 0 ou 1, la proportion de 1 étant ce qu’on cherche à déterminer (un sondage de taille n est ici le tirage au hasard –et avec remise– de n individus dans une population de taille N),

– 100 simulations d’un sondage de taille 100 dans la même population ,

– 100 simulations d’un sondage de taille 400 dans la même population ,

– 100 simulations d’un sondage de taille 1000 dans la même population .

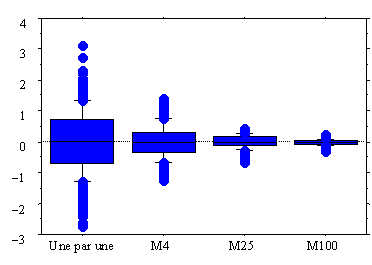
La deuxième figure représente des mesures de hauteur d’eau dans un barrage par rapport à un niveau fixé : on met 100 appareils qui mesurent cette hauteur d’eau ; on a essayé quatre sortes d’appareils de mesure :

– ceux qui font une seule mesure,

– ceux qui font  4 mesures et donnent leur moyenne,

– ceux qui font 25 mesures et donnent leur moyenne,

– ceux qui font 100 mesures et donnent leur moyenne.

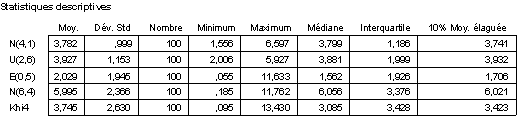
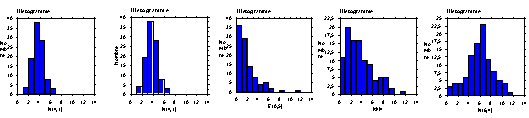
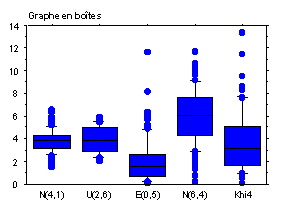
Les deux exemples situés ci-dessus sont spectaculaires et aisés à interpréter. Pour des séries de données quelconques, interpréter un diagramme en boite demande un peu d’expérience et d’honnêteté pour ne pas transformer en affirmation théorique une observation lue sur un diagramme, que ce soit un histogramme ou un diagramme en boîte. Ci-dessous, nous présentons pour des séries de taille 100 simulées à partir de modèles classiquement utilisés divers résumés numériques et graphiques qu’on pourra s’exercer à lire : 

– deux séries simulées à partir de lois de Gauss de moyenne 4 et 6 et de variance 1 et 4 et une série simulée à partir de la loi uniforme sur 1,6. Ces lois sont symétriques autour de leur moyenne : l’espérance et la médiane théorique coïncident et les graphiques théoriques sont symétriques.

– une série simulée à partir de la loi exponentielle d’espérance 2 et une série simulée à partir d’une loi du khi-deux à 4 degrés de libertés : ces lois n’admettent pas de symétrie.

Enfin, à ce propos et pour sa propre formation, l’enseignant pourra utiliser le logiciel SEL (voir annexe). Plus précisément, il pourra :

– dans l’applet située à la page « diagrammes en boite » du lexique voir comment fluctuent ces diagrammes lorsqu’on tire des échantillons au hasard dans un série de données réelles (tailles d’enfants de 6 ans).

– dans l’applet de simulations « diagrammes en bâtons, histogrammes et quantiles » superposer les histogrammes, fonctions de répartitions, fonctions quantiles et diagrammes en boîtes de différentes lois classiques avec celles d’échantillons simulés.

– dans l’applet ajustement par quantiles, visualiser une technique classique d’ajustement de lois à des données.

Annexe : les logiciels SEL et SMEL

Ces logiciels ont pour origine la question suivante :
Comment se servir des outils proposés par le Web pour l’auto formation ou l’enseignement ?
Une réponse possible réside dans la mise à disposition de logiciels interactifs et dont la structure permet à la fois une mise à jour aisée et la transposition dans d’autres domaines.
Le domaine choisi est la statistique ; un premier logiciel SEL (statistique en ligne) est destiné à l’auto formation des enseignants de sciences des lycées et collèges et concerne la statistique descriptive :

http://www.inrialpes.fr/sel

Un second logiciel, SMEL, qui englobe le premier, contient aussi des éléments de base de statistique inférentielle :

http://www.math-info.univ-paris5.fr /smel

Ces deux logiciels sont structurés en quatre couches : une couche articles (26 articles dans SMEL), une couche lexique, une couche cours, une couche simulation. Dans les articles, les mots du lexique (environ 200 dans SMEL :  loi normale, variance, loi de probabilité, etc.)  sont cliquables : apparaît alors la page correspondante du lexique (page html), où le mot est brièvement défini et où figure dans certains cas une applet  interactive (applet en java le plus souvent construite sur un jeu de données réelles accessibles à partir de la page d’accueil du logiciel ; les graphiques comportent des curseurs mobiles et des fenêtres à contenus modifiables) ; dans cette page  il y a de plus des fenêtres à menu déroulant :

– une fenêtre Voir aussi permet d’accéder directement à des mots en lien avec celui de la page ouverte,

– une fenêtre Plus de détails  renvoie à un paragraphe du cours (où les mots du lexique sont aussi cliquables),

– une fenêtre Lecture renvoie aux articles ayant trait au contenu de la page.

Enfin, un renvoi à la couche simulations propose des applets de simulations (comparaison d’estimateurs, loi des grands nombres, analyse de variance, tests, diagrammes, etc..).

Les pages de logiciel sont écrites automatiquement à partir d’un programme contenant tous les éléments à mettre dans cette page, sauf l’applet qui est spécifique du mot concerné dans la plupart des cas.

Chaque utilisateur se définira peu à peu des parcours de formation à l’intérieur du logiciel et grâce à l’interactivité pourra expérimenter soit à partir d’un jeu de données soit avec des données simulées. Ainsi, l’article « courbes de croissance » ouvre le chemin à un travail sur la loi de Gauss Le néophyte pourra se familiariser avec les éléments de base de la statistique descriptive (quantiles, écart-type, divers diagrammes, etc.), voir ce que signifie le loi des grands nombres (et le contre-exemple de la loi de Student de paramètre 1), avoir une idée de ce qu’est l’analyse de la variance, et le moins néophyte pourra s’étonner devant les résultats proposés dans l’applet « variance biaisée et non biaisée » …..

Les logiciels SEL et SMEL sont téléchargeables et…gratuits !