| Statistiques inférentielles |
| Stage « Enseignement de la statistique au lycée » Équipe académique mathématiques. D’après « Itinéraire Statistiques et Probabilités », Collection Ellipse. Bordeaux, juin 2001 |
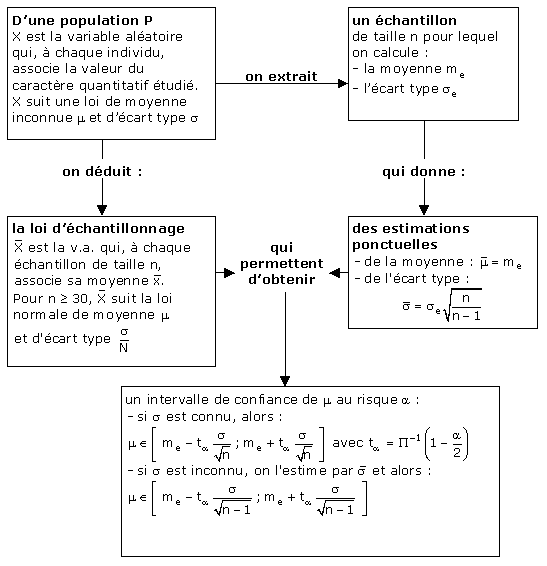
1. Estimation, échantillonnage d’une moyenne

2. Estimation, échantillonnage d’une fréquence
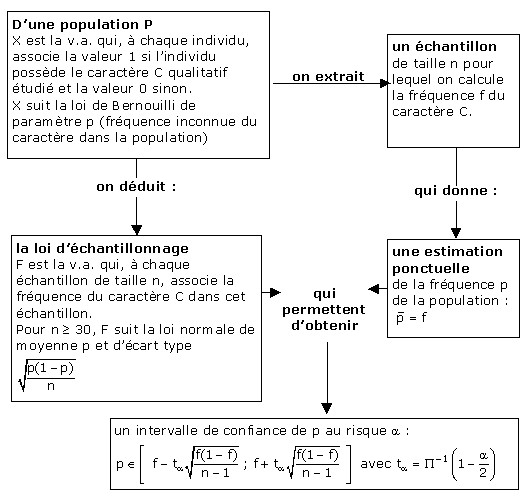
3. Étude des fréquences
Considérons une population P d’effectif N, très grand, dans laquelle
nous nous proposons d’étudier un caractère qualitatif C.
Désignons par X la variable aléatoire qui, à tout élément de P associe la valeur
1 si cet élément possède le caractère C et la valeur 0 s’il ne le possède pas.
Soit p la fréquence ou le pourcentage du caractère C dans la population.
3.1. Constitution d’un échantillon
Prélevons, dans la population P, un échantillon aléatoire de taille
n et désignons par K la variable aléatoire qui, à cet échantillon, associe le
nombre des éléments qui possèdent le caractère C et par F la variable aléatoire
qui, à cet échantillon, associe la fréquence f du caractère C.

3.2. Distribution d’échantillonnage des fréquences
Soit l’ensemble de tous les échantillons de taille n, issus de la
population.
Les fréquences f1, f2, … fi,… constituent une
série statistique appelée distribution de fréquences.
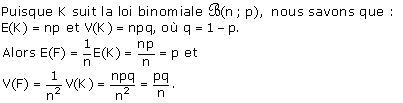
Le théorème de la limite centrée permet alors d’énoncer le résultat suivant, noté (P6) :
Si on prélève des échantillons aléatoires d’effectifs n, où n ³ 30, dans une population non nécessairement normale, dans
laquelle la fréquence du caractère étudié est p, la distribution des fréquences,
notée F, de ces échantillons suit approximativement la loi normale
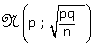 .
.
3.3. Estimation ponctuelle
Le biais sur la fréquence du caractère est l’erreur commise quand
on remplace la fréquence, p, du caractère dans la population par la fréquence,
f, du caractère observé sur un échantillon. C’est la variable aléatoire, notée
e, définie par e = p - F.
Alors E(e)
= p - E(F). Or E(F) = p d’après (P6 ), donc E(e) = 0.
Par suite f est un estimateur sans biais de p.
3.4. Intervalle de confiance
 .
.
Si on fixe un seuil de risque a (donc un seuil de confiance 1 - a), il existe un
réel unique ta(que
l’on détermine à l’aide de la table de la loi normale centrée réduite) tel que :
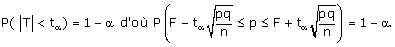
Or p est inconnu et intervient au niveau des bornes de son propre encadrement.
Une méthode consiste à remplacer p sous les radicaux par son estimateur sans biais qui est f.
 .
.
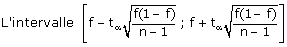
est l’intervalle de confiance de p au seuil de risque a (ou au seuil de confiance 1-a).
Une autre méthode consiste à utiliser le résultat suivant :
Sur l’intervalle [0 ; 1] le produit f(1-f) est maximal
si
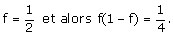
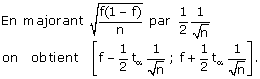
L’élargissement de cet intervalle n’est considéré comme acceptable
que si f est compris entre 0,3 et 0,7.
Dans le cas particulier où a = 0,05 on a ta »
1,96 que l’on peut majorer par 2.
On peut alors énoncer le résultat suivant :
Si f est compris entre 0,3 et 0,7 un intervalle de confiance de p, au risque
de 5%, est
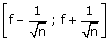 .
.
Exercices
1. De quoi attraper le bourdon
On a mesuré la longueur de chacune des abeilles d’un échantillon de taille 100 pris aléatoirement parmi la population d’une ruche donnée. On a les résultats suivants :
| Longueur en mm |
[3,5 ; 4,5] |
[4,5 ;5,5] |
[5,5 ;6,5] |
[6,5 ;7,5] |
[7,5 ;8,5] |
[8,5 ; 9,5 ] |
[9,5 ;10,5] |
| Effectif |
1 |
2 |
23 |
46 |
24 |
3 |
1 |
Les résultats seront donnés sous forme décimale arrondie au centième le plus proche.
1) Calculer une approximation de la moyenne m et de l’écart type s de cet échantillon.
2) Estimer la moyenne et l’écart type de la longueur d’une abeille de la ruche.
3) On appelle L la variable aléatoire qui, à chaque abeille de cette ruche, associe sa longueur en mm. On admet que L suit une loi normale de moyenne m et d’écart type s que l’on pourra remplacer par sa valeur estimée.
a) On désigne par 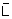 , la variable aléatoire qui
, à chaque échantillon de taille 100, associe sa moyenne. Quelle est la loi
de
, la variable aléatoire qui
, à chaque échantillon de taille 100, associe sa moyenne. Quelle est la loi
de 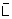 ?
?
b) En utilisant les résultats obtenus pour l’échantillon étudié, déterminer un intervalle de confiance de la moyenne m de la population au risque de 5%.
2. Toujours plus haut
On se propose d’ étudier, dans une population de grand effectif, la taille d’adolescents de 13 à 14 ans. On suppose que la variable aléatoire X donnant la taille d’un adolescent est une variable aléatoire gaussienne de moyenne m et d’écart type s.
1) Un échantillon de 36 adolescents choisis au hasard dans la population étudiée donne les résultats suivants :
| Taille |
[130,135[ |
[135,140[ |
[140,145[ |
[145,150[ |
[150,155[ |
[155,160[ |
[160,165[ |
| Effectif |
1 |
4 |
7 |
10 |
8 |
4 |
2 |
Les résultats seront donnés sous forme décimale arrondie au dixième le plus proche.

2) Afin d’améliorer la connaissance de m, on décide d’augmenter la taille de l’échantillon. À partir de quel entier N0 obtiendra-t-on un intervalle de confiance d’amplitude inférieure à 1 cm, avec le seuil de confiance 98% ?
3. Ballottage favorable
À la veille d’une consultation électorale opposant deux candidats,
on a interrogé 400 électeurs constituant un échantillon de la population concernée
par ce scrutin.
54% d’entre eux ont déclaré avoir l’intention de voter pour LAMER Michel.
1) On suppose que les opinions ne se modifient pas entre la date du sondage et celle du scrutin.
a) Déterminer, au risque 1%, la fourchette dans laquelle se situe la proportion du corps électoral favorable à LAMER Michel.
b) Peut-on considérer dans ces conditions, que LAMER Michel a 99% de chances d’être élu ?
2) Quelle devrait être la taille minimale de l’échantillon pour pouvoir affirmer, avec la même proportion d’électeurs favorables à LAMER Michel, que celui-ci a 99% de chances d’être élu ?