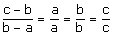
exemple : 5, 9 et 13.
Les Médiétés |
Équipe Académique Mathématiques, |
Présentation de trois médiétés ou moyennes par Nicomaque
Nicomaque est un mathématicien ayant vécu environ 200 ans avant
JC.
Voici comment il présente les différentes moyennes ou médiétés :
Soient trois grandeurs : a, b, c avec a < b < c.
Ces grandeurs sont en :
Médiété arithmétique si :
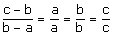
exemple : 5, 9 et 13.
On dit alors que b est la moyenne arithmétique de a et c.
Médiété géométrique si :
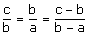
exemple : 7, 21 et 63.
On dit alors que b est la moyenne géométrique de a et c.
Médiété harmonique si :
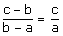
exemple : 3, 4 et 6.
On dit alors que b est la moyenne harmonique de a et c.
Application
A partir de ces trois définitions on peut :
1) Retrouver l’écriture classique des moyennes :
Moyenne arithmétique m telle que :
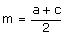
Moyenne géométrique g telle que : g² = ac,
Moyenne harmonique h telle que :
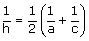 .
.
2) Montrer que trois nombres sont en médiété harmonique si et seulement si leurs inverses sont en médiété arithmétique.
3) Montrer que l’on a la relation :
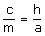
et donc : g² = hm.
4) Montrer enfin qu’on a toujours 0 < a < h < g < m < c.
Construction à la règle et au compas de ces trois nombres
Les trois moyennes obtenues à partir de a et c sont constructibles de par leur définition. Leur construction est l’occasion d’un petit exercice de géométrie dans le triangle rectangle.
On construit bout à bout les segments [OC] et [CA] de longueurs
respectives c et a.
Le nombre m sera la longueur OM avec M milieu de [OA].
On construit alors le demi-cercle de rayon m et de centre M. La perpendiculaire à [OA] passant par C coupe le demi-cercle en H1. Alors g correspond à CH1. On construit ensuite H projeté orthogonal de C sur MH1. la longueur HH1 représente h.
Ces résultats se démontrent facilement à l’aide de triangles semblables et d’utilisation des résultats obtenus dans la première partie.
Avec ce document on trouvera une figure GéoplanW dans laquelle on peut piloter a et c au clavier et où sont affichés a et c ainsi que m, g et h.