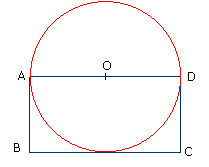
Compléter le texte ci-dessous, qui doit permettre de reproduire la figure ci-contre.
Tracer un rectangle ABCD de longueur 8 cm et de largeur 4 cm.…
Différents types d’évaluation |
Réunion nouveaux programmes 6e |
Exercice 1
Dans un nombre de 8 chiffres 1 □ 9 □ 9 □ 5 □ on doit remplacer les cases par des chiffres pour que le nombre obtenu soit divisible par 2 ; 5 et 9.
Combien de nombres différents remplissant ces conditions peut-on fabriquer ?
Exercice 2
Donner la définition de la médiatrice d’un segment.
Exercice 3 (Transmath p.195)
a) Construire un rectangle ABCD tel que AB = 8 cm et AD = 5 cm.
b) Sur le segment [AB], placer le point E tel que AE = 6 cm. Sur le segment [AD] placer le point F tel que AF = 3 cm.
c) Construire le symétrique du rectangle ABCD par rapport à la droite (EF).
Exercice 4
Dessiner, si cela est possible :
a) un triangle qui a deux angles aigus ;
b) un triangle qui a trois angles aigus ;
c un triangle qui a deux angles obtus ;
d) un triangle qui a un angle droit et un angle obtus ;
e) un triangle qui a un angle plat.
Exercice 5
| Compléter le texte ci-dessous, qui doit permettre de reproduire la figure ci-contre. Tracer un rectangle ABCD de longueur 8 cm et de largeur 4 cm.…
|
|
Exercice 6
Sans effectuer les calculs, entourer le résultat qui vous semble exact :
| 234 x 11,5 = |
269,1 |
962,15 |
2691 |
| 8725 x 0,92 = |
8027 |
88,75 |
802,7 |
| 126 : 12 = |
100,5 |
10,5 |
15 |
| 258 : 1032 = |
4 |
774 |
0,25 |
Exercice 7
M. Quat’sou a fait construire un coffre-fort (un pavé droit de longueur 1,20 m, de largeur 1,20 m et de hauteur 0,76 m). Il veut y enfermer des briques en or (pavés droits de 15 cm sur 8 cm et 6 cm).
1. Peut-il couvrir exactement le fond du coffre en les rangeant toutes dans le même sens bien à plat ?
2. Comment M. Quat’sou doit-il faire pour mettre le nombre maximal de briques dans le coffre ?
Exercice 8
Six personnes mangent ensemble au restaurant. Toutes ont choisi le menu du jour. Elles commandent, en plus, deux bouteilles de vin à 6,45 € l’une et six cafés à 1,95 € l’un.
Le montant s’élève à 90 €.
Quel est donc le prix du menu du jour ?
Exercice 9
Le sel correspond à 3% de la masse de l’eau de mer.
Quelle est la masse de sel que l’on peut obtenir avec 250 kg d’eau de mer ?
Exercice 10
Quel est l’âge du professeur de maths de la classe de 6e C sachant que si on divise son âge par 3 et si on retire 7 au résultat, on obtient 8 ?
Exercice 11
Un premier bouquet de fleurs est composé de 3 iris et 4 roses ; il coûte 4,80 €.
Un second bouquet de fleurs est composé de 5 iris et 6 roses ; il coûte 7,50 €.
Calculer le prix d’un iris et celui d’une rose.
Exercice 12 (Transmath p.25)
Dire si les affirmations suivantes sont vraies ou fausses. Expliquer la réponse.
VRAI |
FAUX |
|
| Le chiffre des dixièmes du nombre 148,25 est le double de son chiffre des dizaines. |
||
|
|
||
|
|
||
| 3,05 est égal à 3,5. |
||
| Un millefeuille a 3 cm de haut. S’il avait réellement 1 000 feuilles, chaque feuille aurait 0,03 mm d’épaisseur. |
||
| Aucun nombre décimal ne peut s’intercaler entre 12,5 et 12,6. |
||
| 27 dixièmes c’est plus que 3,5. |
||
| 0,5 < 2,51 < 2,501 < 2 051 |
||
|
|
Exercice 13 (Bréal p.218)
| a) Observe le cerf-volant ABCD et ses codages. Reproduis-le sur ta feuille. b) Tu vas démontrer que les points C, I et D sont alignés. Recopie et complète : – CA … CB donc le point C est un point de la médiatrice du segment […] – DA … DB donc le point D est un point de … – Le point I est le … du segment [AB]. Donc I est un point de … – Donc les points C, I et D sont sur la … du segment […], c’est-à-dire que les points C, I et D sont …
|
|
Exercice 14
On transporte 5 tonnes de sable avec un camion en 3 voyages.
À chaque voyage le camion chargé est pesé.
Au premier voyage, il pèse 3,650 t ;
au deuxième voyage, il pèse 2,650 t ;
au troisième voyage, il pèse 3,950 t .
Quel est le poids du camion vide ?