Présenté par Anne Hirlimann
mise à jour 05 décembre 1999
Télécharger ce document (format Word, compressé autodécompactable, 138 Ko)

Objectifs :
Niveau : 3ème
Type d'activité : Travaux dirigés en salle informatique
Logiciels utilisés : GeospacW (CREEM / CNAM - SDTETIC diffusé par le CRDP de Reims) et un tableur
Auteur : Nouvelle version de la séquence réalisée par l'équipe des experts-Mathématiques auprès de la SDTETIC
Ce document présente une séquence dont les fiches professeur et élève et les fichiers informatiques sont téléchargeables sur le serveur du ministère à l'adresse : http://www.educnet.education.fr/math/
Apports des logiciels :
Le logiciel "GeospacW" permet :
- de vérifier tous les calculs demandés ;
- de conjecturer la nature d'un triangle par exemple en examinant un plan particulier ;
- de faire tourner les objets géométriques sur l'écran par des actions simples de touches afin de choisir certaines orientations qui permettent de mieux voir les propriétés géométriques de la figure ;
- de relever des mesures de longueur, d'aire et de volume pour différentes positions de la figure.
Le tableur permet, en dégageant les élèves des calculs numériques, tout en leur demandant d'indiquer les méthodes de calcul à mettre en œuvre, de se consacrer à l'observation des résultats et aux conjectures
Remarques générales sur le déroulement de la séquence :
L'alternance du travail papier/crayon et de l'utilisation de l'ordinateur permet de mener conjointement expérimentation, observation, conjecture et réflexion mathématique.
Le logiciel GeospacW donnant des valeurs approchées des calculs demandés, il est indispensable d'engager avec les élèves une réflexion sur les valeurs exactes et les valeurs approchées.
En complément de cette séquence, on peut proposer aux élèves un travail sur le calcul littéral en utilisant par exemple un logiciel de calcul formel.
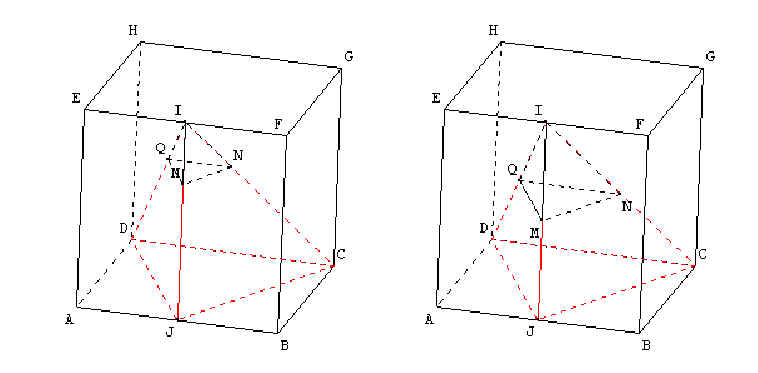
Enoncé : ABCDEFGH est un cube dont l'arête mesure 2 cm. I est le milieu de [EF] et J est le milieu de [AB]. Certains segments sont tracés en pointillés car ils sont cachés. Est-il possible de voir [CD] en trait plein en faisant tourner la figure ? Est-il possible de voir [DI] en trait plein en faisant tourner la figure ? |
|
Geospacw permet de visualiser une figure dans l'espace sous différents points de vue.
Conjecturer la nature du triangle JCD. |
|
GeospacW permet d'examiner une figure dans un plan particulier et donc de voir en vraie grandeur les figures planes.
Calculer les valeurs exactes de JC et JD. Comparer les valeurs approchées données par la calculatrice avec les résultats fournis par "GeospacW". |
|
Geospacw donne des valeurs approchées des longueurs que l'élève peut comparer aux résultats fournis par la calculatrice.
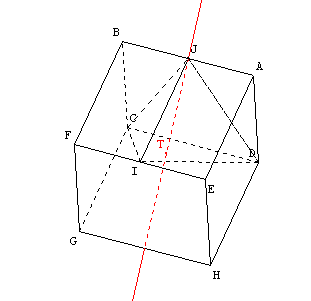
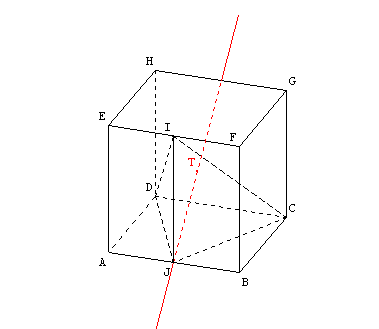
On pose le solide sur la face IDC. Soit [JT] la hauteur du tétraèdre relative à la base IDC. Calculer la valeur exacte de l'aire du triangle IDC. En déduire la valeur exacte de JT.
Cette partie est particulièrement délicate car les élèves éprouvent de grandes difficultés à comprendre que le volume d'un tétraèdre peut se calculer de trois fašons différentes selon le triangle de base choisi (la hauteur du tétraèdre relative à la base étant alors différente selon les cas)
M est à présent un point variable sur le segment [IJ].
Faire varier le point M sur [IJ] à partir de I à l'aide des flèches verticales haut et bas.
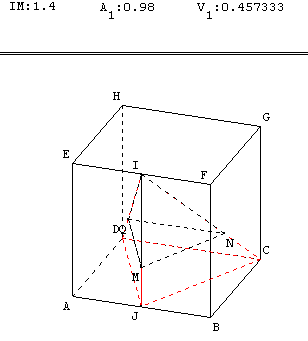
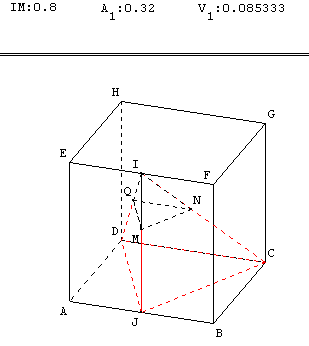
Pour différentes positions de M, compléter sur une feuille de calcul du tableur les colonnes d'un tableau dans lequel figurent IM, A1 (aire du triangle MNQ) et V1 (volume du tétraèdre IMNQ).
On obtient alors le tableau suivant :
IM |
A1 |
V1 |
0,2 |
0,02 |
0,001333 |
0,4 |
0,08 |
0,010667 |
0,6 |
0,18 |
0,036 |
0,8 |
0,32 |
0,085333 |
1 |
0,5 |
0,166667 |
GeospacW permet de faire varier la position d'un point sur un segment et d'obtenir la mesure d'une aire ou d'un volume.
Cette partie est plus expérimentale. En effet, il s'agit de constater les effets d'une réduction sur des longueurs, des aires et des volumes en déplašant un point mobile sur un segment. L'ordinateur permet alors de multiplier les cas de figure et d'obtenir les différents calculs. Les élèves doivent alors découvrir les formules du cours.
A l'aide du tableur :
A désignant l'aire du triangle JCD, 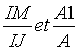 calculer
pour les différentes valeurs de IM relevées dans le tableau
calculer
pour les différentes valeurs de IM relevées dans le tableau
Conjecturer la relation entre ces deux rapports.
V désignant le volume du solide IJCD), calculer pour les différentes valeurs de IM relevées dans le tableau
![]()
et conjecturer la relation entre
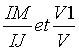
IM |
A1 |
V1 |
IM/IJ |
A1/A |
V1/V |
0,2 |
0,02 |
0,001333 |
0,1 |
0,01 |
0,001 |
0,4 |
0,08 |
0,010667 |
0,2 |
0,04 |
0,008 |
0,6 |
0,18 |
0,036 |
0,3 |
0,09 |
0,027 |
0,8 |
0,32 |
0,085333 |
0,4 |
0,16 |
0,064 |
1 |
0,5 |
0,166667 |
0,5 |
0,25 |
0,125 |
Le tableur permet ici, en dégageant les élèves des calculs numériques, tout en leur demandant d'indiquer les méthodes de calcul à mettre en oeuvre, de se consacrer à l'observation des resultats et aux conjectures.