Aire d'un triangle

Michel BENASSY, académie de Bordeaux

mise à jour 05 décembre 1999

780

Télécharger l'exposé décrit ci-dessous
(format RTF Word + fichier Géoplan Windows, le tout compressé au format ZIP, 745 Ko)

Activité 1 : (tri1.g2w)

Objectifs

Après avoir rappelé la formule de calcul de l’aire d’un triangle ABC, visualiser certaines ‘’déformations’’ de ce triangle ne modifiant pas son aire.

Mémoriser ces situations sous forme d’images mentales ‘’dynamiques’’.

Déroulement

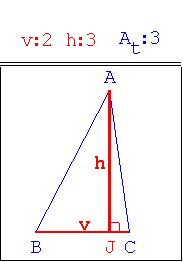
Touche 1 (bascule) : crée un triangle ABC ( BC = v).
Touche J (bascule) : crée [AJ] (AJ = h).
On note A_t l’aire de ABC. Les valeurs de v , h et A_t sont affichées.
v pilotable (touche V). h pilotable (touche H).

Faire varier v . Constater la variation de A_t .
Faire varier h . Constater la variation de A_t .
Recourir éventuellement à l’activité complémentaire 2.

On s’intéresse alors à certaines ‘’déformations’’ de ce triangle ne modifiant pas son aire.

Dans la suite de l’activité les valeurs de v et de h sont fixées donc l’aire A_t est constante.

On pourra afficher ou ne pas afficher les valeurs de v , h et A_t .

En conservant [AJ] fixe, déplacer à la souris
le point B de telle sorte que les droites (BC) et (AJ) restent perpendiculaires.
Faire apparaître la droite d = (BC) grâce à une construction par étapes (touche D).
En conservant [BC] fixe, déplacer à la souris le point A de telle sorte que les droites (BC) et (AJ) restent perpendiculaires.
La touche T visualise le lieu des points .
Faire apparaître la droite d’ grâce à la construction par étapes (touche D).
Résumer ce qui précède en utilisant la configuration ci-contre :
Déplacer à la souris les points A puis B et indiquer aux élèves que la mémorisation de cette image mentale dynamique sera utile pour résoudre les petits problèmes proposés ensuite dans les activités 2 . 3 et 4 .
On pourra traiter ces activités en gardant cette configuration à l’écran (fenêtre en mosaïque).

Activité 1 suite : (tri1.g2w)

Objectifs

Reconnaître certains triangles de même aire :
- soit en identifiant des ‘’configurations statiques’’.
- soit en ayant recours aux ‘’images mentales dynamiques’’ évoquées en début d’activité.
Décomposer ou recomposer des aires.

Fonctions

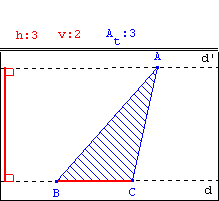
Touche 2 (bascule) : crée un triangle EFG tel que : E î d’ ; F î d ; G î d avec FG = BC = v.
La distance BF = x est pilotable ( touche X ).
Touche B (resp. C) amène F en B (resp. en C).
Touche E (resp. F ou G) fait apparaître ou disparaître le nom du point E (resp. F ou G).
Touche 3 (étapes): quand F est en B, crée [AE], H intersection de [AC] et [BE] ; visualise BHC.

Quelques situations exploitables

Exemple 1

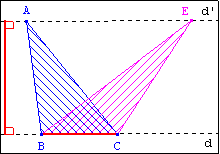
Statique : Si (AE) est parallèle à (BC) alors les triangles BAC et BEC ont la même aire.

Dynamique : Si E se déplace sur une droite parallèle à (BC) alors le triangle BEC conserve la meme aire.

Exemple 2

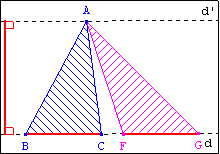
Statique : Si les points B, C, F, G sont alignés avec BC = FG alors les triangles BAC et FAG ont la même aire.

Dynamique : Si [FG] se déplace sur une droite alors le triangle AFG conserve la même aire.

Retour sur l’exemple 1

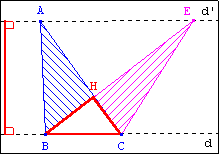
Théorème dit ‘’du papillon’’ :
Si ABCE est un trapèze non croisé de bases [AE] et [BC] dont les diagonales se coupent en H alors les triangles ABH et ECH ont la même aire.

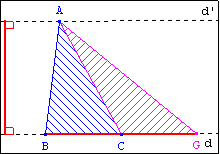
Retour sur l’exemple 2

Rôle d’une médiane :
La médiane [AC] du triangle ABG partage celui-ci en deux triangles ABC et AGC de même aire.

Activité 1, compléments 1 (tri1.g2w)

Objectifs

Rappeler la relation entre aire d’un triangle et aire d’un parallélogramme.
Visualiser certaines ‘’déformations’’ du parallélogramme ABCD ne modifiant pas son aire.

Mémoriser ces situations sous forme d’images mentales ‘’dynamiques’’.

Déroulement

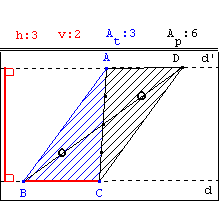
Touche 4 (bascule) : crée le parallélogramme ABCD tel que D soit le symétrique de B par rapport au milieu de [AC] et affiche son aire A_p .

Faire varier h . Constater la variation de A_p .
Faire varier v . Constater la variation de A_p .

A l’aide de la souris :
- Déplacer A sur d’et constater l’invariance de l’aire A_p.
- Déplacer [BC] sur d (grâce au point B)et constater l’invariance de l’aire A_p.

Activité 1, compléments 2

Objectifs

h étant fixé (resp. v étant fixé ), représenter graphiquement dans un repère ( O , I , J ) l’aire A_t du triangle ABC en fonction de v (resp. en fonction de h).

Interpréter les représentations graphiques.

Déroulement

Charger tri1c. g2w en ouvrant les fenêtres en mosaïque :

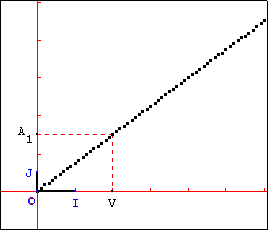
Touche V : crée le point de coordonnées ( V ; A_l ) .

h étant fixé, piloter v dans tri1. g2w pour observer les variations de A_l en fonction de v

Pour obtenir la représentation graphique de A_l en fonction de v , activer le mode trace ( Touche T ).

Touche H : crée le point de coordonnées ( H ; A₂ ) .

v étant fixé, piloter h dans tri1. g2w pour observer les variations de A₂ en fonction de h.

Pour obtenir la représentation graphique de A₂ en fonction de h , activer le mode trace ( Touche T ).

Activité 2 (tri2.g2w)

Objectif

Utiliser les méthodes vues dans l’activité 1 pour traiter un problème.

Ecran initial

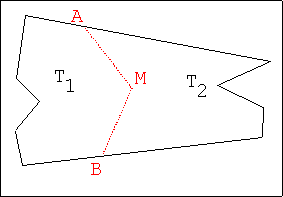
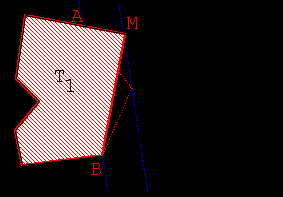
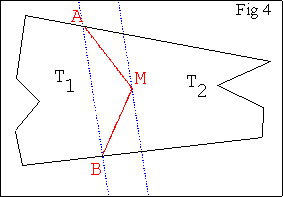
Deux voisins possèdent les terrains T₁ et T₂ .
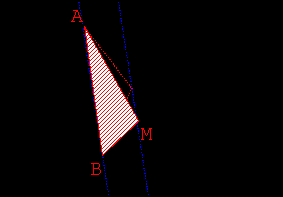
Ils souhaitent remplacer leur ‘’clôture-ligne brisée-AMB’’ par une "clôture-segment" ayant une extrémité en A (ou en B) de telle sorte que chacun conserve l’aire de terrain qu’il avait au début.

La touche 1 (resp. 2) hachure T₁ ( resp.T₂ ).

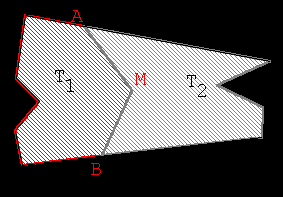
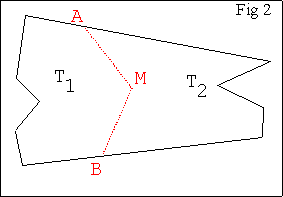
Déroulement de l’activité

L’aide à la conjecture se fait par le biais d’une construction par étapes (touche E).

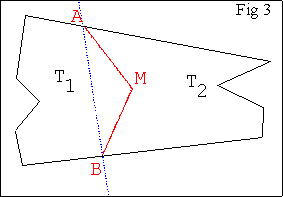
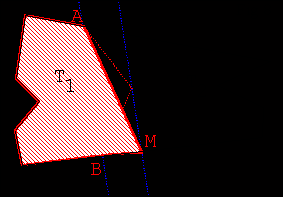
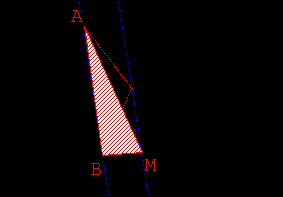
Tracer (AB) pour faire émerger le triangle ABM
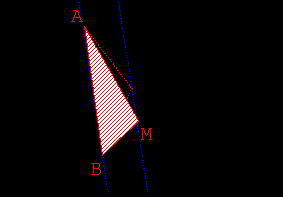
Utiliser ensuite les résultats de l’activité 1 pour transformer le triangle AMB en un triangle de même aire dont un sommet appartienne à l’une des droites frontières.
On peut hachurer le triangle ABM (touche 3).

La touche B (bascule) efface les tracés annexes. La touche M replace le point M en position initiale.

Activité 3 (tri3.g2w)

Objectif

Utiliser les méthodes vues dans l’activité 1 pour traiter un problème.

Ecran initial

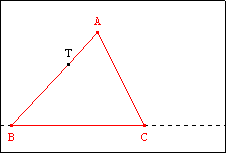
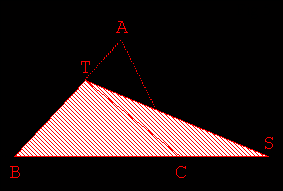
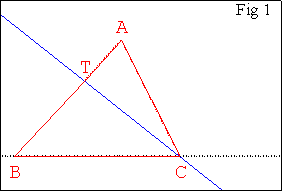
Soit un triangle ABC. T est un point de [AB].

Construire un point S de [BC) tel que les aires des triangles BAC et BTS soient égales.

Déroulement de l’activité

L’aide à la conjecture se fait par le biais d’une construction par étapes (touche E).

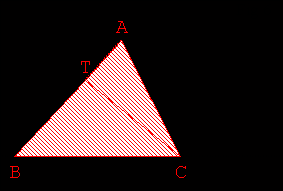
Tracer (TC) pour faire émerger le triangle ATC (Fig 1.).

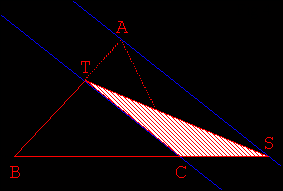
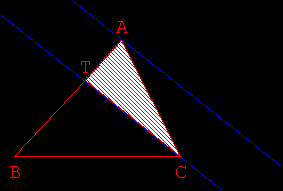
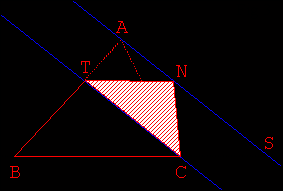
Utiliser ensuite les résultats de l’activité 1 pour transformer le triangle ATC en un triangle TNC puis TCS de même aire, avec S point de [BC) (Fig 2. 3. 4.).

La touche B (bascule) efface les tracés annexes (Fig 5.).

La touche T hachure en deux temps les triangles TNC et BTC (Fig 2. 5.).

La touche A (resp. S) amène le point N en A (resp. en S) (Fig 5. 6.).

Activité 4 (tri4.g2w)

Objectif

Utiliser les méthodes vues dans les activités 1 et 3 pour traiter un problème.

Ecran initial

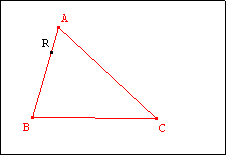
Soit un triangle ABC et R un point de [AB].

Construire un point M appartenant à [BC] ou à [AC] de telle sorte que le segment [RM] partage le triangle ABC en deux polygones de même aire.

Discuter suivant la position de R sur [AB].

Déroulement de l’activité

Pour poser le problème, la touche 4 crée une demi-droite [Ru).
- Lorsque [Ru) coupe [AC] en T, la touche 5 crée le triangle ART (Fig 1.).
- Lorsque [Ru) coupe [BC] en T (différent de C) , la touche 6 crée le quadrilatère ACTR (Fig 2.).
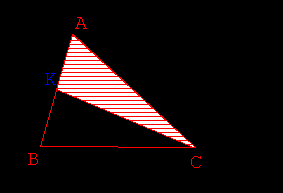
- Le cas particulier où R est situé en K milieu de [AB] est obtenu grâce à la touche K (Fig 3.).

L’aide à la conjecture se fait par le biais d’une construction par étapes (touche E).
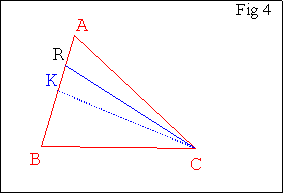
Tracer la médiane [KC] et le segment [RC] (Fig 4.).

Ici R appartient à [KA] et le point M cherché appartiendra à [BC].
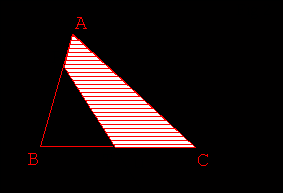
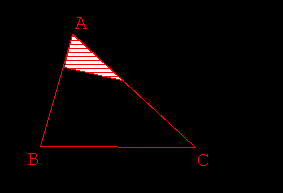
La touche 2 (resp. 1) permet de hachurer le triangle KRC (resp. ARC) (Fig 5.).
La somme des aires des triangles ARC et KRC est égale à la moitié de l’aire du triangle ABC (Fig 6.).

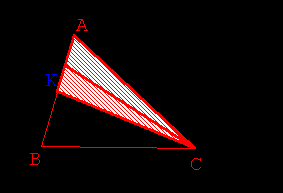
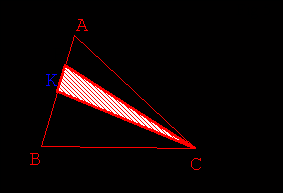
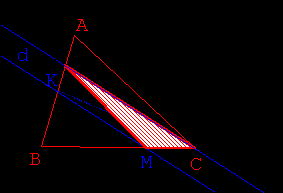
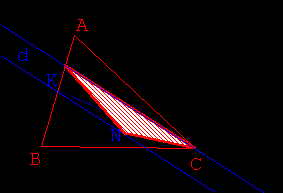
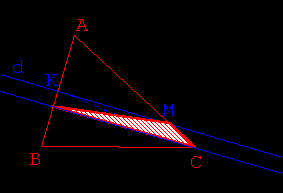
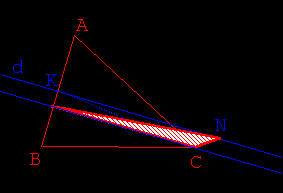
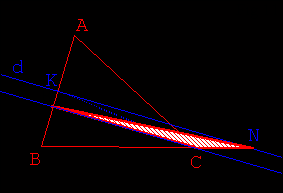
Utiliser ensuite les résultats de l’activité 1 (Fig 7.) pour transformer le triangle KRC :
- en un triangle NRC de même aire (N étant un point non nommé de la droite d parallèle à (RC) contenant K)
- puis en un triangle MRC de même aire, M étant l’intersection de d et de [BC] (Fig 8. 9.).

La touche A suivie de M nomme M le point d’intersection de d et de [BC].
La touche 0 ramène le point N en K.
Lorsque M est apparent la touche M l’efface.

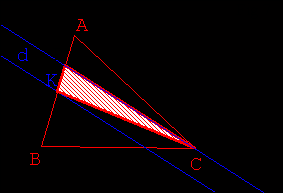
La touche E suivie de 1 fournit la solution ( Fig 10.) : le point M de [BC] est tel que le triangle BRM et le quadrilatère ACMR ont la même aire.

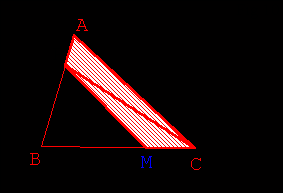
Revenir à la situation de la figure 9. Déplacer à la souris le point R pour l’amener sur [BK] (Fig 11.).

Utiliser ensuite les résultats de l’activité 1 pour transformer le triangle RNC en un triangle MRC de même aire, M étant l’intersection de d et de [AC] (Fig 11. 12.).

La touche B suivie de M nomme M le point d’intersection de d et de [AC] (Fig 13.).
La touche 0 ramène le point N en K.
Lorsque M est apparent la touche M l’efface.

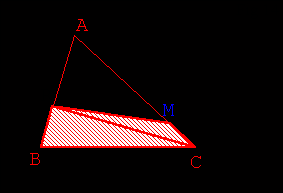
Les triangles KRC et RMC ont la même aire.

La somme des aires des triangles KRC (donc RMC) et BRC est égale à la moitié de l’aire du triangle ABC.

La touche E suivie de 3 fournit la solution ( Fig 14.) : le point M de [AC] est tel que le triangle ARM et le quadrilatère BCMR ont la même aire.

Annexe : document - élève

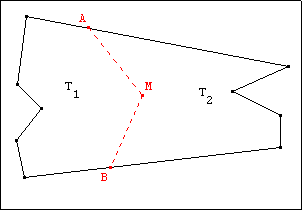
Activité 2

Deux voisins possèdent les terrains T₁ et T₂ .
Ils souhaitent remplacer leur ‘’clôture-ligne brisée-AMB’’ par une ‘’clôture-segment’’ ayant une extrémité en A (ou en B) de telle sorte que chacun conserve l’aire de terrain qu’il avait au début.

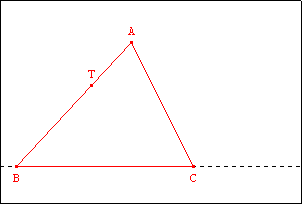
Activité 3

Soit un triangle ABC. T est un point de [AB].

Construire un point S de [BC) tel que les aires des triangles BAC et BTS soient égales.

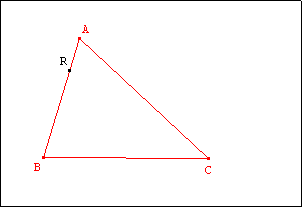
Activité 4

Soit un triangle ABC et R un point de [AB].

Construire un point M appartenant à [BC] ou à [AC] de telle sorte que le segment [RM] partage le triangle ABC en deux polygones de même aire.

Discuter suivant la position de R sur [AB].