La nature de ces triangles n’est pas révélée aux élèves.
Le triangle ABC est dessiné en vert, le triangle DEF est dessiné en rouge.
Les côtés de ces triangles n’ont aucun point commun pour l’instant.
mise à jour 05 décembre 1999
Il s’agit de présenter de manière dynamique la notion d’axe de symétrie d’une figure.
L’expérience prouve que la présentation par des moyens classiques au tableau est difficile à mettre en œuvre et parfois trop peu parlante pour les élèves. L’utilisation de l’ordinateur en classe, en " tableau électronique " permet d’améliorer la présentation de cette notion.
La séquence présentée prend place après l’étude de la symétrie axiale et des propriétés classiques de conservation. Les élèves connaissent également les figures transformées des figures de base par symétrie axiale.
L’essentiel du travail présenté pendant la séquence porte sur les triangles isocèles. On utilise le logiciel GeoplanW (Fichier trisocel .g2w)
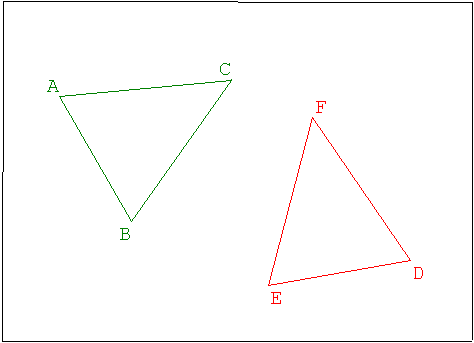
| L’activité débute par la présentation de deux
triangles isocèles (fig. 1). La nature de ces triangles n’est pas révélée aux élèves. Le triangle ABC est dessiné en vert, le triangle DEF est dessiné en rouge. Les côtés de ces triangles n’ont aucun point commun pour l’instant. |
|
Une discussion s’engage pour conjecturer :
La vérification des ces conjectures peut entraîner des mesures de longueurs à l’aide de la règle graduée ou d’angles à l’aide du rapporteur.
On peut utiliser les commandes au clavier :
Lorsque ces longueurs et ces angles sont affichés, on fait remarquer :
Pour terminer cette première partie, on pilote le triangle ABC pour que les deux triangles soient effectivement superposés. Enfin, on dissocie de nouveau les deux triangles.
Il doit alors se dégager l’idée que le triangle rouge est obtenu à partir du vert par une symétrie axiale. (La seule "transformation" connue des élèves de 6ème )
On demande alors aux élèves comment ils vont trouver l’axe de cette symétrie. Cette recherche fait appel à l’identification des points qui doivent se correspondre par la symétrie en question. De nombreuses notions déjà vues dans les lešons précédentes doivent pouvoir être réutilisées.
| En particulier, le cas de figure ou deux côtés des
triangles ABC et DEF se coupent permettent de retrouver la propriété que possèdent des
droites symétriques de se couper sur l’axe de symétrie. Suivant l’orientation que prennent les débats, on construira (ou on demandera à un élève de le faire) une médiatrice ou une droite passant par les points d’intersection de deux côtés. La figure peut alors se présenter ainsi (fig. 2): |
|
La phase suivante consiste à mettre en évidence comment se comporte l’axe de symétrie lorsque les triangles superposables sont effectivement superposés.
On pilote alors le triangle ABC pour superposer à nouveau les deux triangles, et on
fait constater alors que l’axe de symétrie est alors devenu une droite remarquable
du triangle ABC isocèle en C : la médiatrice de la base [AB].
Le triangle ABC ainsi obtenu est donc son propre symétrique dans
la symétrie ayant pour axe la médiatrice de sa base [AB]. (fig.3)
Il s’agit maintenant de trouver l’axe de symétrie sans modifier comme précédemment le triangle ABC, c’est à dire l’axe de symétrie d’un triangle iscocèle donné.
| On fait alors apparaître deux poignées P1 et P2 sur la
médiatrice, en utilisant la commande A au clavier. (fig. 4) Le déplacement des poignées P1 et/ou P2 permet alors de superposer les deux triangles sans modifier le triangle ABC, et par conséquent DEF (fig.5) On a donc bien trouvé l’axe de symétrie DU TRIANGLE ABC isocèle en C donné. |
|
Pour montrer que l’existence de l’axe de symétrie est bien lié à la nature du triangle ABC, on va faire apparaître un élément supplémentaire dans la figure et examiner l’effet de cette adjonction sur l’existence de l’axe de symétrie.
| La commande x , combinée avec l’utilisation des touches
fléchées du clavier, permet de "dédoubler" les côtés du triangle ABC. On obtient alors la figure ci-contre : La figure verte et la figure rouge ont les mêmes
dimensions. Elles sont superposables. |
|
Le prolongement est naturellement la recherche sur papier de l’axe de symétrie
d’un triangle isocèle.Un document préparé à l’avance est distribué alors
aux élèves.
L’élève dispose d’un triangle ABC isolèle en C .On demande de construire la
médiatrice de la base [AB], et de vérifier que la figure symétrique de ce triangle par
raport à cette médiatrice d est le triangle ABC lui-même.
On peut à cette occasion réinvestir des acquis antérieurs : définition de la
symétrie, propriétés de la médiatrice d’un segment, pliage autour de la
médiatrice, etc…
Prolongements de l’activité.
On a opéré sur des triangles icocèles. On aborde le même travail pour un triangle scalène ABC, pour faire constater l’absence d’axe de symétrie.
(Fichier triangle.g2W)
Des commandes permettent de rendre ce triangle :
On passe ensuite à des figures plus complexes :
Pour chacune de ces études, on préparera la figure de départ, pilotable par un nombre variable de poignées, sa figure symétrique par rapport à une droite P1P2 pilotable, comportant les commandes d’affichage nécessaires.