![]() n°5, mars 1998
n°5, mars 1998
J’ai découvert MATh.en.JEANS l’année dernière à mon entrée en seconde au lycée Montaigne. Nous étions cinq dans le lycée à participer à ce club : un groupe de deux élèves de terminale et un groupe de trois élèves de seconde, chaque groupe travaillant sur un sujet différent et se réunissant environ une heure et demie par semaine en présence d’un professeur.
Notre groupe a travaillé sur les fractions égyptiennes (inverses d’entiers naturels), cherchant à montrer que, pour tout entier naturel n, les fractions 4/n et 5/n pouvaient s’écrire comme somme de trois fractions égyptiennes.
Nous avons exposé nos résultats par trois fois au cours de séminaires auxquels participaient aussi les équipes du lycée Sud Médoc (Le Taillan) avec lequel nous étions jumelés dans le cadre du club, ainsi qu’un chercheur chargé de commenter nos résultats et, au besoin, d’aiguiller nos recherches. Les séminaires servaient eux-mêmes à préparer le 8ème congrès national de l’association MATh.en.JEANS qui s’est déroulé à Paris en mars 1997, dans un esprit de convivialité, toute notion d’évaluation, de compétition ou de récompense étant exclue.
Pour 4/n, par exemple, nous avons cherché à résoudre notre problème en distinguant différents cas de n de la forme 4m, 4m + 1, 4m +2, 4m + 3.
![]() .
.
![]() .
.
Pour n = 4m
+ 1 et
n =
4m +3, nous avons cherché, pour décomposer
4/n en 1/x
+ 1/y
+ 1/z,
à prendre pour 1/x la fraction inférieure à
4/n s’en approchant le plus, obtenue pour
x =
E(n/4) + 1,
puis on tente de décomposer
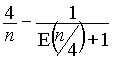 .
.
Dans le cas oł n =
4m +
3, on obtient :
![]() .
.
Par contre, dans le cas oł n = 4m + 1, on est amené à distinguer les cas m pair et m impair.
Si m = 2p + 1, on obtient :
![]() .
.
Mais si m = 2p, il faut distinguer de nouveaux cas (p = 3q, p = 3q + 1 et p = 3q + 2). On trouve une décomposition dans les deux derniers cas et il reste le cas non résolu p = 3q (ou n = 24q +1).
Nous avons cependant trouvé une méthode de décomposition manuelle permettant de décomposer quelques fractions appartenant aux cas n = 24q + 1.
Cette méthode consiste à transformer la fraction 4/n en une fraction équivalente 4d/nd telle que la somme de trois diviseurs a, b, c de nd vaille 4d (il faut 4d ³ nd sinon la méthode ne marche pas).
Ainsi : 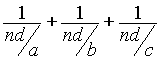 fournit la décomposition de 4/n.
fournit la décomposition de 4/n.
Par exemple, pour 4/193 (avec d = 50, a = 193, b = 5 et
c = 2) on obtient : ![]() .
.
Bien que cette méthode soit très vite limitée pour n très grand, elle présente un double intérêt :
- elle fournit une méthode rapide aux ordinateurs pour décomposer de telles fractions ;
- elle offre un nouvel axe de recherche (que nous n’avons pas pu beaucoup
explorer) : en effet si on arrive à prouver que pour toute fraction 4/n,
il existe un nombre d tel que la somme de trois diviseurs de nd
vaille 4d, alors le problème est résolu.
Pour ma part, je garde un excellent souvenir de ma participation
à ce club, ce qui m’a bien entendu amené à poursuivre une deuxième année
cette activité avec un nouveau problème.