 ,
Applications des mathématiques
,
Applications des mathématiquesOdile Moreau, professeur au lycée Victor Louis de Talence
n°6, mai 1998
| Algèbre linéaire et comptabilité nationale |
| |
 ,
Applications des mathématiques ,
Applications des mathématiquesOdile Moreau, professeur au lycée Victor Louis de Talence n°6, mai 1998 |
Une nouveauté des programmes de mathématiques de Terminale ES, qui entreront en application à la prochaine rentrée, est l’apport de connaissances de géométrie dans l’espace ; elles permettront aux futurs étudiants de mieux aborder l’algèbre linéaire dont voici une application à un problème issu des Sciences Économiques et Sociales - c’est un des exemples présentés en atelier lors des journées inter-académiques de Toulouse (cf. RéciproqueS n°5). Ce texte a été directement inspiré par le livre " Comptabilité nationale " d’Édith Archambault aux éditions Economica, suite à un travail interdisciplinaire avec G. Caplanne, professeur d’économie au Lycée Montaigne de Bordeaux.
Pour les comptes d’une nation, on regroupe les unités de production par branches (agriculture, industrie, commerce...) et par produits (produits de l’agriculture, de l’industrie, etc.)
Un tableau à double entrée, appelé tableau d’entrées-sorties (T.E.S.) - qui permet par ailleurs de définir le produit intérieur brut - résume, pour chaque branche et chaque produit : la production, la consommation, les importations, les exportations, les droits de douane, les marges, la T.V.A., les variations de stock...
Toutes ces quantités sont exprimées en unité monétaire : on ne compte pas les kilos de farine mais les francs que fourniront ces kilos de farine.
Étudions un T.E.S. très simplifié, ne comportant que trois branches (I : agriculture, II : industrie, III : services) et trois produits (de l’agriculture, de l’industrie et des services), et négligeant les relations avec l’extérieur, les marges, les stocks, la T.V.A...
Pour chaque produit et chaque branche il faut distinguer la consommation finale et la consommation intermédiaire (CI) ; par exemple, de la farine utilisée pour nourrir du bétail que l’on vendra est comptée comme consommation intermédiaire, tandis que de la farine utilisée pour les crêpes familiales est comptée comme consommation finale.
T.E.S.simplifié :
(en milliards de francs, chiffres de 1975)
| branche produit |
I |
II |
III |
S |
Consommation |
Production |
| I |
150 |
10 |
30 |
190 |
110 |
300 |
| II |
35 |
390 |
80 |
505 |
495 |
1000 |
| III |
15 |
100 |
90 |
205 |
395 |
600 |
Les consommations intermédiaires sont notées dans le tableau encadré d’un trait double. La première colonne de ce tableau se lit ainsi : l’agriculture utilise pour 150 Mds F de produits agricoles, pour 35 Mds F de produits de l’industrie, pour 15 Mds F de services. La première ligne se lit : des produits de l’agriculture, 150 Mds F sont réutilisés par l’agriculture, 10 Mds F servent à l’industrie, 30 Mds F sont utilisés par les services et 110 Mds F sont utilisés pour la consommation finale. La production totale agricole fournit donc 300 Mds F (150+10+30+110).
Pour utiliser ce tableau, son créateur Leontief (prix Nobel d’économie 1973) a émis l’hypothèse suivante :
Les coefficients techniques
![]()
restent constants d’une année sur l’autre.
La matrice A des coefficients techniques est donc :
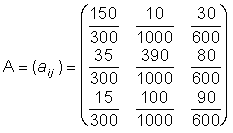
On obtient alors AX = S .
Or X = S + Y. D’où X = AX + Y et Y = (I - A)X où I est la matrice unité.
Conséquences : si l’année prochaine nous avons une production X, nous savons que nous pourrons disposer d’une consommation finale Y = (I - A)X. Si nous prévoyons pour l’année prochaine une consommation finale Y, pour y faire face il faudra une production X = (I - A)-1 Y.