La simulation numérique pour la science et la technologie

, Applications des mathématiques Jean Ovadia - Ingénieur au CEA / CESTA Commissariat à l’Énergie Atomique Centre d’Études Scientifiques et Techniques d’Aquitaine n°7, décembre 1998

La simulation numérique a vu le jour en 1943 à Los Alamos, dans le cadre du projet Manhattan qui a abouti à la création des premières armes nucléaires. Depuis, les progrès de l’analyse numérique, conjugués à la puissance croissante des ordinateurs, ont permis d’étendre considérablement le domaine d’application de la simulation numérique. Aujourd’hui presque toutes les sciences de la matière, du vivant, de l’économie y ont recours.

L’étude d’une situation réelle repose tout d’abord sur une étude physique (ou biologique, économique…), qui aboutit à un modèle plus ou moins proche de la réalité, et qui s’exprime souvent par l’ensemble d’un système d’équations aux dérivées partielles, de conditions initiales, et de conditions aux limites ; par exemple, la diffusion thermique dans un parallélépipède métallique est traduite par :

• l’équation 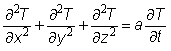, où T est la température à la date t au point de coordonnées (x, y, z)  et a une constante dépendant du matériau ;

• la donnée de la température initiale en chaque point à l’intérieur du parallélépipède ;

• la donnée de la répartition de température en chaque point de la surface du parallélépipède (répartition imposée par l’extérieur).

La simulation numérique nécessite de remplacer le système d’équations continues par un ensemble d’équations discrètes (voir exemple). Une programmation permet ensuite de traduire en langage accessible à un ordinateur l’algorithme de résolution. Le rôle de l’analyse numérique est de démontrer la convergence de la solution approchée vers la solution " exacte ".

Exemple

Soit à résoudre l’équation différentielle notée (1) : y’ = y, où y est une fonction de x qui vaut 1 en x = 0 (condition initiale).

Si e est petit, on peut assimiler y’(x) à (y(x+e )-y(x)) / e et l’équation (1) devient : y(x+e ) »  y(x)_*(1+e ) ; connaissant y(0), on peut calculer y(e ), puis y(2e ), et ainsi de suite. On calcule en fait les termes d’une suite (y_n) (définie par
y_n = y(n*e )) selon la relation de récurrence : y_n+1 = y_n*(1+e ) et y₀ =1.

On a donc bien remplacé le système continu de départ (x parcourt 3 ) par un système discret (on calcule y(x) pour les valeurs de x multiples de e ).

La confrontation simulation / expérimentation peut conduire à une remise en cause aussi bien du modèle physique que de la méthode numérique.

Elle constitue un point de rencontre entre physiciens (ou biologistes…) et mathématiciens.

À ses débuts, la simulation numérique avait principalement pour objet de réduire les coûts et les délais, en suppléant à des expériences dont la modélisation était parfaitement maîtrisée. Dans une deuxième étape, elle a contribué à l’innovation technique, en permettant de prendre en compte des modèles physiques plus complets et d’accéder à des informations difficiles à obtenir par les mesures. Maintenant, elle aide également à l’élaboration de nouveaux modèles physiques, par exemple en intégrant par le calcul les effets d’un grand nombre de phénomènes simples.

Les grands projets scientifiques et techniques du CEA sont développés dans le cadre d’une démarche interactive entre théorie, simulation et expérimentation. Par exemple, le projet de laser mégajoule, en cours de réalisation au CEA/CESTA, permettra de réaliser des expériences dans le domaine d’énergie du thermonucléaire (étoiles ou armes) afin d’étudier certains phénomènes physiques.

Les résultats expérimentaux obtenus seront aussi utilisés pour valider différentes parties des modèles physico-numériques employés dans les logiciels de simulation des armes nucléaires. Il sera ainsi possible de mettre au point par le calcul certains dispositifs sans procéder à des expériences globales en vraie grandeur.

Aujourd’hui, les diverses branches des mathématiques appliquées concourent de plus en plus à la compréhension et à l’action sur le réel. Aussi, de nombreux scientifiques partagent-ils l’idée – émise par John von Neumann – que le monde dans sa totalité relève du champ d’intervention des mathématiques.