Trajectoires aériennes

, Applications des mathématiques n°9, mai 1999

Spécialisée dans les essais d'armements aéroportés, la base de Cazaux du Centre d' Essais en Vol est amenée à restituer les trajectoires de différents mobiles à l' aide de moyens optiques au sol ou embarqués.

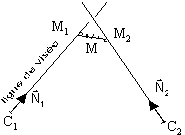
Une des techniques utilisées est la restitution de trajectoires par triangulation. Ce principe nécessite l'observation simultanée du mobile à trajectographier par deux moyens optiques différents, le point recherché se trouvant à l'intersection de leurs lignes de visée.

Dans le cas des mesures sol, des caméras orientables - les cinéthéodolites - manipulées par des opérateurs, enregistrent la trajectoire sur support film ou vidéo. En pratique, les lignes de visée ne se coupent jamais. Aussi considère-t-on que le point cherché est le milieu de [M₁M₂] où (M₁M₂) est la perpendiculaire commune. La plupart du temps, trois caméras, voire quatre, sont mises en œuvre pour pallier une éventuelle défaillance des moyens et choisir à chaque instant le couple garantissant la meilleure précision.

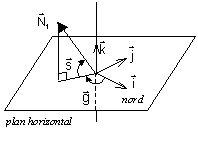
L'axe d'un cinéthéodolite peut subir deux rotations :

• une rotation autour d'un axe horizontal : l'angle axe optique-plan horizontal est appelé site (s) ;

• une rotation autour d'un axe vertical : l'angle de cette rotation, référencé par rapport au nord, est appelé gisement (g).

Les coordonnées du vecteur unitaire sont alors (u₁, v₁, w₁) avec : u₁= cos (s).cos (g), v₁ = cos (s).sin (g) et w₁ = sin (s). Ces mesures effectuées, il convient d'exprimer les coordonnées des points d'observation C₁ et C₂ ainsi que les composantes des vecteurs dans un même repère de référence. Les coordonnées du point M s'obtiennent alors par résolution des équations : ; M est le milieu de [M₁M₂]. Image après image, la trajectoire du mobile est ainsi élaborée, une trajectoire d'une minute trente nécessitant la visualisation de 1800 images. Pour pouvoir déterminer la vitesse et l'accélération du mobile, on procède ensuite à une opération de lissage de la courbe : en utilisant la méthode des moindres carrés, on réalise un ajustement de sept points consécutifs de la trajectoire par un polynôme du second degré.

Bien que relativement anciennes, ces méthodes restent fortement utilisées car elles permettent de restituer une trajectoire avec plus de précision que les radars, et ne nécessitent aucun moyen embarqué comme, par exemple, les récepteurs GPS.