8 minutes 10 secondes de bonheur

, Application des mathématiques Jean Prunin, Commandant de bord Concorde n°10, décembre 1999

Astronome amateur et passionné de tout ce qui se passe dans le ciel et l’espace, j’ai eu l’idée d’utiliser la formidable vitesse du Concorde pour suivre l’éclipse solaire du 11 août 99 et faire durer le phénomène beaucoup plus longtemps qu’au sol, tout en s’affranchissant du risque météorologique.

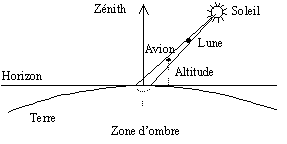
L’étude des éphémérides m’avait montré que la brièveté du moment de totalité était due au fait que l’ombre était animée d’une vitesse de l’ordre de 900 m/s. Le Concorde volant à deux fois la vitesse du son, soit environ 600 m/s à 17 km d’altitude, on devait pouvoir tripler la durée de l’observation puisque la vitesse relative tombait à 300 m/s. On remarquera qu’une éclipse équatoriale est beaucoup plus lente car la différence des vitesses angulaires terre-soleil qui génère le mouvement s’étale sur un grand cercle alors que le rayon du parallèle 50° N n’est que r = R cos L soit 0,64 fois plus petit que le rayon terrestre.

En regardant les circonstances locales d’un peu plus près, je me suis rendu compte qu’il faudrait faire appel à mes souvenirs de trigonométrie du lycée car, bien sûr, la ligne de centralité n’allait pas être la même à 17 km d’altitude qu’au sol, puisque le cône d’ombre était incliné de 39° (hauteur du soleil).

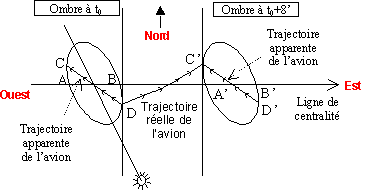
Un simple transport de position permettrait de résoudre ce problème.

En regardant encore plus en détail, j’ai réalisé que même en considérant la terre comme plane sur la centaine de kilomètres occupée par l’ombre, on ne pouvait pas assimiler cette tache à un cercle car l’intersection d’un cône et d’un plan est une ellipse et il a fallu que je retrouve mon cours de Math Sup sur les coniques pour m’en sortir. J’ai pu déterminer les caractéristiques de cette ellipse.

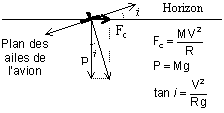
Au lieu de se déplacer le long de la ligne de centralité, j’ai eu l’idée de partir du point D (le plus en avant) pour sortir au point C’ (le plus en arrière) et ainsi parcourir dans l’ombre la distance D’C’ »  DC beaucoup plus longue que BA. Encore un peu de mathématiques pour déterminer le rayon de virage et finalement le paramètre fondamental de pilotage qui en découlait : l’inclinaison de l’avion.

Bilan : au lieu des 2 minutes 10 secondes de totalité au sol, nous avons triplé, grâce à la vitesse de l’avion, soit 6 minutes 30 secondes, et en suivant l’arc de cercle DC’ nous sommes passés à 8 minutes 10 secondes, presque quatre fois le temps de base.

De plus, le fait de faire un virage continu à 6° d’inclinaison diminuait la hauteur apparente du soleil et améliorait l’azimut qui augmentait avec la variation du cap et rendait l’observation de plus en plus facile.

L’outil mathématique s’est ainsi révélé nécessaire pour optimiser la trajectoire mais sans la formidable vitesse de ce bel oiseau qu’est le Concorde, rien de tout cela n’aurait été possible.

Le spectacle des étoiles et planètes qui se rallumaient dans un ciel indigo, de la courbure de la terre parfaitement visible à cette altitude sur laquelle fuyait cette petite ellipse sombre valait bien 

• une louche de mathématiques ;
• une cuillère à café de bon sens ;
• un doigt d’intuition ;
• un zeste d’expérience ;
• un grain de réalisme ;
• une pincée de chance et mille autres choses encore que je ne saurais vous raconter ici…