Anecdote

, Carte blanche à Michel Mendès France, Professeur émérite, Université Bordeaux 1 n°15, mai 2001

Il y a une vingtaine d’années, Mike Keane célèbre mathématicien américain, me montrait une très jolie démonstration de l’irrationalité de  qui, bien différente de l’approche classique, ne fait pas appel à la divisibilité. Plusieurs années plus tard nos chemins se croisèrent à nouveau au Chili. « Tu sais, me dit-il, ta démonstration de l’irrationalité de  me fascine ! Où l’as-tu trouvée ? ». Confirmation que les mathématiciens sont bien souvent distraits (et si c’était moi qui étais dans la lune ???).

Voici donc cette preuve.

On observe d’abord que 1 < 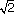 < 2.

Supposant que 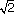 est rationnel, il existe un entier q ³ 1 minimal tel que q 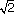 î N.

Considérons alors le nombre q’ = q 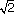 - q < q.

On remarque que q' 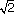 = 2q - q  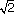î N, ce qui est absurde puisque 0 < q ’ < q.

CQFD