 ,
Pédagogie
,
PédagogieÉquipe académique Mathématiques
n°15, mai 2001
| À propos de raisonnement |
| |
 ,
Pédagogie ,
PédagogieÉquipe académique Mathématiques n°15, mai 2001 |
Certains élèves ressentent parfois la démonstration comme un exercice formel où l’on prouve des résultats qui leur paraissent évidents. L’étude de problèmes ouverts doit contribuer à surmonter cette difficulté. Durant cette activité, l’émergence d’idées conduit à exprimer des conjectures précises ; pour discerner les vraies des fausses, la recherche de preuves constitue alors un enjeu réel.
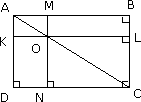 |
Dès la sixième, demandons aux élèves de réaliser une figure du type ci-contre, puis de comparer les aires des quadrilatères NOKD et MBLO. Un débat s’installe entre ceux qui pensent qu’elles sont égales et ceux qui en doutent. Une démonstration aidera à établir une conclusion incontestable. |
Il est également essentiel de faire comprendre que la production de nombreux exemples n’est pas une preuve tandis que celle d’un seul contre-exemple en est une. Cherchons le nombre de diviseurs de n 2 – n + 11, avec n entier. L’étude des cas n = 0, n = 1… laisse supposer qu’il y a, pour tout entier n, exactement deux diviseurs. La production d’un contre-exemple permettra de rejeter cette proposition mais il faudra aller jusqu’à n = 11. La découverte de l’erreur est un moment important dans la formation de l’élève : si toutes les conjectures étaient justes, la démonstration ne serait plus nécessaire.
L’arithmétique permet, dès la classe de cinquième, de travailler un autre type de raisonnement : la disjonction des cas.
Avec les théorèmes de Pythagore et de Thalès, on peut introduire en classe de quatrième le raisonnement par l’absurde. On a pu voir dans l’exercice 2 de l’enquête du n°14 de Réciproques que ce type de raisonnement est difficile pour certains élèves. Il paraît toutefois important d’y consacrer du temps et de tirer profit de son rôle formateur, notamment pour dépasser les confusions possibles entre propriété directe, réciproque et contraposée.
La notion d’équivalence, avec l’utilisation du « si et seulement si » ; est abordée en classe de seconde où l’on introduit les notions de condition nécessaire et de condition suffisante.
En série scientifique, certaines recherches de lieux géométriques nécessitent une démarche par double inclusion ou un raisonnement par analyse-synthèse ; ce dernier type de raisonnement permet aussi de traiter des questions d’existence et d’unicité ou des problèmes de construction. Enfin, le raisonnement par récurrence sera abordé en classe de terminale à l’occasion de l’étude des suites notamment.
À l’issue de la résolution d’un problème, la rédaction de la démonstration demeure un travail important. Lorsque l’expression de l’élève est maladroite, il est très difficile de distinguer l’erreur de compréhension de la mauvaise maîtrise de la langue. Dans l’exercice 1 de l’enquête de Réciproques, certains d’entre nous ont vu une erreur de raisonnement et l’ont lourdement sanctionnée par 1 sur 5 alors que d’autres n’ont vu qu’une maladresse de rédaction et ont attribué 4 sur 5. Pour l’exercice 2, où l’élève semble confondre réciproque et contraposée, les notes vont de 1,5 à 5. La dernière solution satisfait la majorité des collègues ; malgré sa maladresse d’écriture, l’élève montre qu’il a raisonné correctement.
Critiquer, infirmer, justifier une affirmation, exprimer correctement ses idées, dépassent largement le cadre des Mathématiques et relèvent de la formation générale de l'individu. L'étude, tout au long de la scolarité, de situations d'apprentissage suffisamment variées participe à cette dynamique.
Raisonnement par l’absurde
Raisonnement par analyse-synthèse
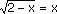 .
.Raisonnement par disjonction des cas
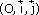 , rechercher l’ensemble des
points M(x, y) tels que |x| + |y| < 4.
, rechercher l’ensemble des
points M(x, y) tels que |x| + |y| < 4.Utilisation du contre-exemple
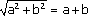 est fausse.
est fausse.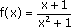
Raisonnement par double inclusion
