Premières notions sur les graphes en série ES

n°16, décembre 2001

La théorie des graphes

C’est pour résoudre le célèbre problème des « ponts de Königsberg » que Leonhard Euler a posé les fondements de la théorie des graphes, qui s’est surtout développée depuis la deuxième moitié du 19^e siècle et connaît une grande effervescence depuis les années 30.

Quelles applications ?

La théorie des graphes est un outil de modélisation et donc de résolution de problèmes, utilisée dans un grand nombre de disciplines (mathématiques, physique, économie, etc.).

Concrètement, elle s’applique dans de nombreux domaines :

modélisation de réseaux électriques, informatiques et de télécommunications,
résolution de problèmes de routage de transports,
résolution de problèmes de minimisation de coûts,
résolution de problèmes d’affectation (emplois du temps, mutations, rotations d’équipes…).

Selon quelle démarche ?

La résolution de problèmes de graphes est un domaine essentiellement développé par les informaticiens pour lesquels un graphe est une structure de données, tout comme un arbre ou un tableau.

On traduit un problème concret, dont on pense qu’il peut être traité par cette théorie, en termes de graphes.
Il devient alors un problème de la théorie des graphes que l’on essaye de résoudre en le faisant entrer dans une catégorie de problèmes connus.
Si ce n’est pas le cas, il alimentera la recherche jusqu’à ce qu’il devienne un problème résolu !

Exemple 1- Sur les ponts

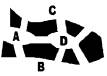Königsberg, 1736 :
Sept ponts enjambent la Pregel, reliant quatre quartiers de la ville.
Les habitants se demandent s’il existe un trajet leur permettant d’emprunter une seule fois tous les ponts.

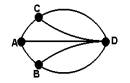Euler modélise le problème et ouvre ainsi une nouvelle théorie.
Les quartiers sont les sommets du graphe, les ponts les arêtes. Il y a quatre sommets (l'ordre du graphe est 4), au sommet A arrivent trois arêtes (le degré de A est 3).
Le problème posé induit deux questions : existe-t-il un trajet partant d'un point donné, passant par toutes les arêtes une et une seule fois (chaîne eulérienne) ? Ou bien existe-t-il une chaîne eulérienne revenant au point de départ (cycle eulérien) ?

Le théorème d'Euler énonce qu'un graphe admet une chaîne eulérienne si et seulement si tous ses sommets sont de degré pair, sauf au plus deux. Un graphe admet un cycle eulérien si et seulement si tous ses sommets sont de degré pair.

A Königsberg, rebaptisée depuis Kaliningrad, il y a deux nouveaux ponts, l'un entre B et C et l'autre entre B et A. Y a-t-il une chaîne eulérienne ? Où faudrait-il construire un autre pont pour obtenir un cycle eulérien ?

Exemple 2- À l’école

Une école doit faire passer des tests à quatre élèves : Adrien, Sophie, Charlotte et Matthieu. Sept disciplines sont concernées : les mathématiques, la physique, la biologie, le français, l'anglais, l'espagnol et l’histoire.

Adrien doit passer les mathématiques, la physique et l'anglais, Sophie les mathématiques, la biologie et le français, Charlotte les mathématiques, l'anglais et l'espagnol et Matthieu la physique, le français et l'histoire.

Quel est le nombre minimal de plages horaires à prévoir pour qu'aucun élève n'ait à passer deux tests simultanément ?

On peut modéliser la situation par le graphe suivant :

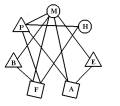les sommets représentent les disciplines, les arêtes relient les disciplines dont les tests ne peuvent avoir lieu simultanément.
Les plages horaires sont représentées par des formes géométriques (ou par des couleurs).
On attribue à chaque sommet une forme, deux sommets adjacents ne pouvant avoir la même. Le sous-graphe complet M, A, E (tous les sommets sont adjacents) nécessite trois formes. Le dessin prouve que trois sont suffisantes pour le graphe. Ainsi le nombre chromatique du graphe est trois.

Si Adrien doit aussi passer le test d’histoire, le nombre chromatique devient supérieur ou égal à quatre.

Un dessin prouve qu'il est de quatre.

Les graphes en série ES

Terminale ES – spécialité à la rentrée 2002.
Temps imparti : environ 40% de l’horaire.
Enseignement entièrement fondé sur la résolution de problèmes ; « place à l’initiative des élèves avec un temps nécessaire de tâtonnements et d’essais ».

Objectifs

S’ouvrir à de nouveaux raisonnements, à un autre regard sur les mathématiques.
Premières approches de situations concrètes (vie professionnelle).
Quelques applications du calcul matriciel développées dans l’option de 1re ES.
Réinvestissement en TPE.

Divers documents sur les graphes sont disponibles sur ce serveur