Des TICE au collège pour quoi faire ?

, Pédagogie n°17, mars 2002

Un outil pour visualiser

Autour d’une pyramide

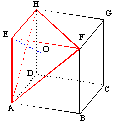
ABCDEFGH est un cube de 6 cm de côté.
On considère la pyramide de base AFH et de sommet E, O le pied de la hauteur de cette pyramide.

Dessiner EAF en vraie grandeur, calculer AF.
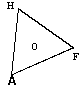
Déterminer la nature du triangle AFH ; le dessiner en vraie grandeur.
Quel rôle joue le point O pour ce triangle ? Calculer AO en utilisant le milieu I du segment [HF].
Calculer EO.

Retrouver le résultat précédent en exprimant le volume de la pyramide de deux façons

Le fichier de cette activité est téléchargeable sur le site académique

L’assistance d’un logiciel de géométrie dans l’espace va permettre une réelle appropriation de la figure, comme étant une représentation d’un objet en trois dimensions. Cet outil donne en effet la possibilité de changer d’angle de vue, de choisir le plan de face, de visualiser le développement d’un solide…

Les élèves pourront ainsi :

- prendre conscience qu’il existe plusieurs représentations du même solide et ainsi identifier les différentes bases de la pyramide et leur hauteur correspondante ;

- choisir une base de la pyramide et la visualiser en vraie grandeur ;

- détecter les angles droits (qui semblent aigus sur la figure initiale) et isoler des triangles rectangles utilisables pour les calculs ;

- identifier les segments de même longueur (qui semblent de longueur différente sur la figure initiale) ;

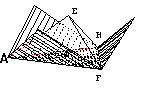
- visualiser le patron de la pyramide en vraie grandeur.

Un tel logiciel permet donc de mieux atteindre les objectifs du programme : voir dans l’espace, être capable d’extraire une figure à partir de la représentation en perspective d’un solide, se construire des images mentales relatives à des situations de parallélisme.

Un outil pour expérimenter

Distance minimale

ABC est un triangle rectangle en A.
M est un point libre sur [BC].
Les perpendiculaires à (AB) et à (AC) passant par M coupent [AB] et [AC] respectivement en P et Q.
La longueur PQ varie-t-elle ?

Si oui, pour quelle(s) position(s) de M est-elle minimale ?

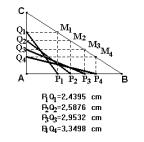
Un logiciel de géométrie plane permet de mener cette activité autour de la notion de distance d’un point à une droite en privilégiant la phase d’expérimentation.

Dans un premier temps, chaque élève pourra mener un travail de recherche, guidé par une fiche de travail ou par des indices donnés pas à pas par le professeur :

- compléter l’imagiciel de départ en construisant les points P et Q ;

- déplacer le point « libre » M, constater que la distance PQ varie bien (affichage de la distance PQ) et observer que la position du point M cherchée semble unique ;

- rechercher cette position sur d’autres triangles rectangles (déplacement de B et C), et tenter de caractériser cette position ; observer la permanence du rectangle MNPQ ;

- tracer le segment [AM], observer que le problème revient à chercher le plus court chemin de A à la droite (BC) (affichage de la distance AM), et préciser sa conjecture.

Dans un deuxième temps, le professeur pourra faire un travail de synthèse avec la classe entière, assisté du logiciel (utilisation d’un rétroprojecteur ou d’un téléviseur relié à l’ordinateur). Les conjectures pourront être testées et la mesure de l’angle 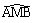 pourra être affichée, pour confirmer que la position cherchée est le pied de la hauteur issue de A.

L’élève abordera ensuite plus facilement la rédaction d’une solution du problème, en s’appuyant sur les images mentales dynamiques qu’il aura mémorisées et qui l’auront aidé à identifier ce qu’il doit démontrer ainsi que les propriétés mises en jeu.

Charger le fichier Géoplan (1,4 Ko ; ne fonctionne qu'avec le logiciel Géoplan)
Dans ce fichier on appelle x la longueur CM et y la longueur PQ.
On considère repère (O, OI, OJ) le point N de coordonnées (x,y).
On peut ainsi tracer la courbe décrite par le point N et "voir" qu'il existe un minimum.

Le commentaire de la figure contient l'énoncé.