,
Pédagogien°21, mai 2003
| Approche historique des maths au collège |
| |
| ,
Pédagogie n°21, mai 2003 |
|
Le Livre I des Éléments d’Euclide est riche en constructions à la règle et au compas. Certaines propositions sont accessibles dès le collège et permettent de mobiliser des propriétés relatives aux triangles et aux parallélogrammes. Ainsi étudions la proposition (cf. Livre I p.44 ) : « Sur une droite donnée et dans un angle donné, appliquer un parallélogramme égal à un triangle donné t » que nous traduisons par : Un triangle ABC, un segment [EF] et un angle
Il s’agit ici de travailler sur la notion d’aire sans effectuer de calculs.  |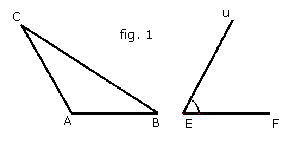
 |
Exercice préliminaire
Nous utiliserons quelques résultats accessibles aux élèves de 5e :
(1) Une diagonale partage un parallélogramme en deux triangles de même aire (cf. Livre I p.34).
(2) Une médiane partage un triangle en deux triangles de même aire (cf. Livre I p.38).
(3) Si les droites (RS) et (UV) sont parallèles alors les triangles RUS et RVS ont la même aire (cf. Livre I p.37).
(4) Les angles opposés d’un parallélogramme ont la même mesure (cf. Livre I p.34).
(5) Deux angles opposés par le sommet ont la même mesure (cf. Livre I p.15).
|
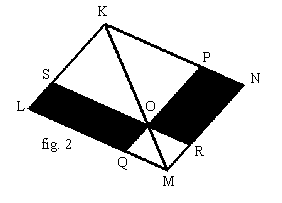
O est un point quelconque de la diagonale [KM] d’un parallélogramme KLMN. La droite parallèle à (KL) passant par O coupe [KN] en P et [LM] en Q. La droite parallèle à (KN) passant par O coupe [KL] en S et [NM] en R. Montrer que les parallélogrammes OSLQ et ORNP ont la même aire (cf. Livre I p.43). |
 |
Retour au problème principal
 |
 |
 |
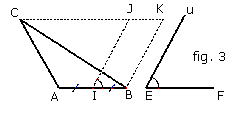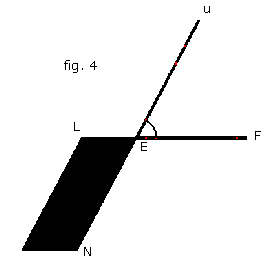Il suffit alors (fig. 4) d’imaginer le parallélogramme ELMN (superposable à KJIB) et le segment [EF] dans les rôles respectifs du parallélogramme OSLQ et du segment [OR] de la figure 2, les propriétés (4) et (5) assurant les alignements voulus.
|
|
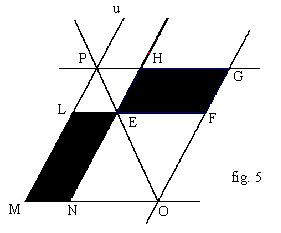
La droite parallèle à (EN) passant par F coupe (MN) en O. La droite (OE) coupe (ML) en P. La droite parallèle à (EF) passant par P coupe [Eu) en H et (OF) en G (fig. 5). On obtient le parallélogramme EFGH attendu. |
 |
L'aventure poétique des mathématique
Au collège Princeteau de Libourne, les élèves d’une classe de 4e travaillent chaque semaine en bi-disciplinarité sur l’histoire des mathématiques, à partir du « Théorème du perroquet » de Denis Guedj.
|
« Les élèves ont lu quelques chapitres que nous
retravaillons avec eux », expliquent Katia Le Menn, Denis Rateau
(Maths) et Jean-Michel Verlot (Français), « soit d’un point de vue
historique ou littéraire (les Grecs, les Égyptiens, la grande Bibliothèque
d’Alexandrie, etc.), soit d’un point de vue mathématique (les fractions
égyptiennes, une démonstration historique du théorème de Pythagore, la
preuve de l’irrationalité de En parallèle, les élèves réalisent des panneaux sur divers thèmes : Thalès, l’histoire des symboles mathématiques, le nombre d’or, etc., effectuant de nombreuses recherches sur Internet. Une frise historique faisant apparaître les principaux mathématiciens est également complétée. « Cet atelier, confie Jean-Michel Verlot, fait prendre peu à peu conscience aux élèves des méandres qui ont abouti à ce qu’ils écrivent dans leurs cahiers. Il permet également de décloisonner les matières littéraires et scientifiques, donnant l’occasion d’aborder, à leur niveau, des notions philosophiques. Les élèves adhèrent bien, l’intervention en binôme étant très porteuse : voir que le prof de Français se débrouille en Maths et réciproquement les réjouit ! » Comble du plaisir pour ces jeunes : ils ont pu rencontrer l’auteur et aborder avec lui maints sujets allant de l’histoire des maths à leurs difficultés de collégiens. |
|
étant donnés,
construire le parallélogramme EFGH de même aire que le triangle ABC et
tel que le sommet H appartienne à [Eu) (fig. 1). 
, etc.) ».
(pour l’unité ou
pour 60) et un chevron 
(pour 10). Ainsi
par exemple,