,
Pédagogien°21, mai 2003
| Approche historique des mathématiques au lycée |
| |
| ,
Pédagogie n°21, mai 2003 |
Les commentaires des programmes recommandent de faire prendre conscience aux élèves que les mathématiques sont une discipline vivante, fruit du labeur et du génie de nombreux individus : connaître le nom de quelques-uns d’entre eux et la période à laquelle ils ont vécu devrait faire partie du bagage culturel de tout élève ayant une formation scientifique. La plupart des idées ont mis longtemps à émerger ; le savoir permet à l’élève de mieux accepter l’importance du temps qu’il devra passer pour se les approprier.
Sans être systématique – la construction d’une notion n’aidant pas toujours l’élève à se l’approprier – une approche historique est conseillée dans certains apprentissages. L’enseignant peut travailler sur un ensemble de textes anciens liés à un même thème, permettant de voir la nature et la formulation des questions à l’origine de certains concepts. Il peut être aussi profitable de repérer sur une chronologie l’évolution des idées.
Christian Drouin, professeur au lycée de Borda à Dax, étudie avec des élèves de 1e S un texte de Torricelli. Plusieurs notions mathématiques de natures très diverses sont ainsi dégagées : variation des définitions des termes mathématiques au cours du temps, réinvestissement de l’équation de la tangente vue en cours, ainsi que diverses notions de logique (un exemple tient-il lieu de preuve ? comment infirmer une propriété ?).
|
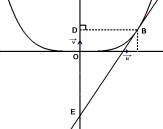
Evangelista Torricelli (1608-1647) fut un mathématicien et physicien disciple de Galilée. Il donne une méthode pour construire une tangente à une courbe C en un point B quelconque de cette courbe. « Qu’on prenne ED égale à la longueur DO multipliée par l’exposant de la parabole, donc quatre fois dans le cas présent et la ligne qui joint EB sera la tangente… » |
 |
 |
Le travail s’effectue en trois parties :
|
Les suites de Héron sont fréquemment utilisées au lycée où souvent l’algorithme est donné a priori. Or, il peut être intéressant de pouvoir justifier historiquement la construction de cet algorithme afin de montrer que la plupart du temps, les formules établies pour ce genre de suites ne sont pas le fruit du hasard, mais sont issues d’une réflexion préalable.
 |
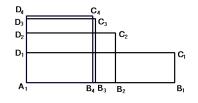L’idée de Héron (1er siècle av. J.-C.) est, à partir d’un rectangle d’aire donnée A et de dimensions L et l (L > l), de construire un nouveau rectangle de même aire que le précédent et dont la longueur est la moyenne arithmétique de L et l. Cette moyenne, atténuant la différence entre les dimensions L et l, rend le deuxième rectangle un peu plus « carré » que le précédent. |
La répétition du processus donne une succession de rectangles (A1BnCnDn) dont les dimensions (rationnelles) Ln et ln vérifient :
|
On démontre alors que les suites (ln) et
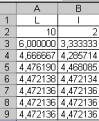
(Ln) sont adjacentes et convergent vers En partant d’un rectangle de dimensions 10 2,
on obtient un quatrième rectangle dont la longueur approche |
 |
On peut noter que cette méthode coïncide exactement avec la méthode de la tangente due à Newton (1642-1727) et appliquée à la fonction f définie par f(x) = x2 - 20.
 |
Les équations ont été largement étudiées par les mathématiciens arabes. Al Khawarizmi (788-850) classe les équations du second degré et les résout par des moyens algébriques. Les solutions sont uniquement positives car elles représentent des longueurs. Omar Khayyâm (1048-1123) établit une classification de celles du troisième degré et affirme qu’elles ne peuvent être résolues que géométriquement, à l’aide d’intersections de coniques dont les propriétés sont bien connues à l'époque. Les solutions ne sont toujours que positives. |
|
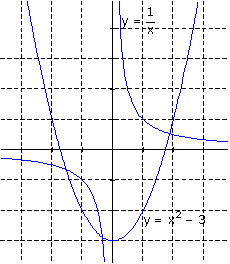
En classe de seconde, où sont introduites les fonctions de référence, ce genre de résolution peut faire l’objet d’une introduction au cours sur les équations. L’équation x3 = 3 x + 1 devient et les solutions sont les abscisses des points d’intersection d'une parabole et d'une hyperbole. |
 |
Réflexion
sur le texte pour amener les élèves à trouver que l’équation de la courbe
est y = x4 .
.
.
à moins de 10
