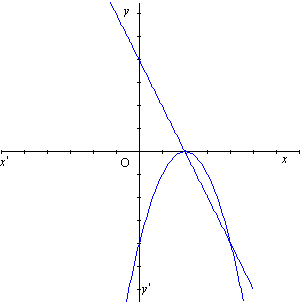
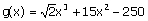 ,
,et C sa courbe représentative obtenue à l’aide d’une calculatrice.
| Deux en une |
| Conjuguer des outils (1) |
| Objectifs | Reconnaître l’existence d’une racine double pour un polynôme en associant procédés algébriques, lecture graphique et méthodes d’analyse. |
| Support | Fonctions polynômes. |
| Organisation | Travail de recherche autonome suivi d’une synthèse partie par partie. |
Problème
A. Si un polynôme admet une racine double...
Soit f la fonction polynôme définie par f(x) = -3x3 + x2 + 7x - 5.
1. Factoriser f(x) et en déduire l'ensemble des racines du polynôme f.
2. Déterminer la fonction f’ dérivée de f, puis les racines du polynôme f’.
3. Que peut-on dire de la racine double de f ?
B. Si une fonction polynôme et sa dérivée admettent une racine commune...
Soit g la fonction polynôme définie
par :
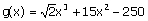 ,
,
et C sa courbe représentative obtenue à l’aide d’une calculatrice.
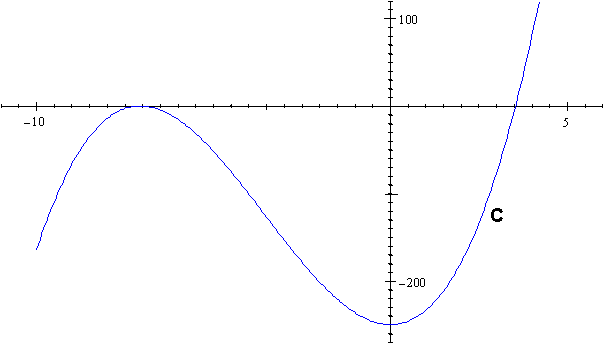
1. a. En observant le graphique, émettre une conjecture sur les racines du polynôme g et donner une valeur approchée pour chacune d’elles. On notera x0 la plus petite de ces racines.
b. Émettre une conjecture sur le nombre dérivé de g en x0.
2. a. Déterminer la fonction g’, dérivée de g, puis les racines du polynôme g’.
b. Vérifier que l’un de ces nombres est racine du polynôme g.
c. En déduire une factorisation de g(x), puis l’ensemble des racines du polynôme g.
3. Que peut-on dire de la racine commune aux polynômes g et g’ ?
Sujet d’étude. Une racine pas si simple
1. Soit f une fonction polynôme de degré supérieur ou égal à deux
telle que f(x) = (x - )2
p(x),
où a désigne
un nombre réel et p une fonction polynôme.
Démontrer que la fonction dérivée de f s’annule
en a.
2. Soit g une fonction polynôme
de degré supérieur ou égal à deux telle que g et sa fonction dérivée g’
admettent une racine commune x0.
Démontrer que g(x) se factorise
sous la forme g(x) = (x - x0 )2q(x),
où q
désigne une fonction polynôme.
3. Énoncer la propriété établie.
4. Applications
a. Retrouver la condition nécessaire et suffisante pour qu’un polynôme du second degré admette une racine double.
b. Factoriser h(x) = 54x4 - 27x3 - 90x2 + 92x - 24 .