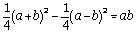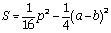En faire un max

Formaliser : mise en fonction (1)
Extrait de "Espace modules première", CRDP d'Aquitaine
Équipe académique de mathématique

 

Objectif Résoudre un problème d’optimisation relatif à un volume : investigation d’une fonction de plusieurs variables ; détermination d’extrema par des procédés algébriques.
Support Fonctions polynômes.
Organisation

La partie A, « rectangle d’aire maximale », très classique, doit être traitée rapidement afin de ménager un temps de recherche personnelle suffisant pour l’étude de la partie B, « pavé de volume maximal ».

En synthèse, les élèves seront invités à reconstituer l’enchaînement de la démarche.

 

Problème

On se propose de démontrer l’existence d’un pavé de volume maximal parmi tous les pavés droits dont la somme des trois dimensions est donnée.

A. Lemme - Rectangle d’aire maximale

Soit un rectangle de dimensions a et b. On désigne par p son périmètre et par S son aire.

1. Vérifier que :
.
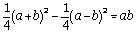En déduire que :
.

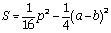2. Démontrer que, parmi tous les rectangles de périmètre donné, le carré est celui dont l’aire est maximale.

 

B. Pavé de volume maximal

1.  Dans cette question, la dimension est fixée.

a.  En utilisant la partie A, caractériser la face ABCD pour laquelle le volume du pavé ABCDEFGH est maximal.

b.  Exprimer, en fonction de c, le volume V(c) de ce pavé.

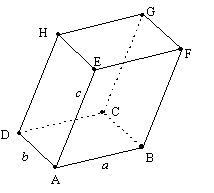On désigne par E l’ensemble des pavés droits dont la somme des trois dimensions est égale à 3.
ABCDEFGH étant un élément de E, on note AB = a, AD = b et AE = c.

 

2. On examine ici le volume V(c) lorsque c décrit l’intervalle ] 0 ; 3 [.

a. À l’aide de la calculatrice, compléter le tableau de valeurs suivant :

c

0,25

0,5

0,75

1

1,25

1,5

1,75

2

2,25

2,5

2,75

V(c)

                      

b. Pour quelle valeur de c le volume V(c) semble-t-il atteindre un maximum ?

c. Factoriser l’expression V(c) - V(1), puis étudier son signe.
En déduire la valeur de c pour laquelle V(c) est maximal.
Quelle est alors la nature du pavé correspondant ?

3. a. On considère un pavé droit (P1) élément de E. Soit (P2) le pavé droit, élément de E, à base carrée et de hauteur égale à celle de (P1). Soit (P3) le cube de côté 1.
Comparer les volumes respectifs V1, V2 et V3  de (P1), (P2) et (P3).

b. Que peut-on en conclure pour les volumes des pavés droits dont la somme des trois dimensions est égale à 3 ?

 

Sujet d'étude. Aires tétra-bornées

Soit OABC un tétraèdre trirectangle * en O tel que  OA = OB = OC = 6.

On a représenté ci-contre :
–   la section MNPQ du tétraèdre par le plan parallèle aux droites (AB) et (OC), et passant par un point M du segment [OA] ;
–   la section NPR du tétraèdre par le plan parallèle au plan (OAB) et passant par le point N.
On note x la distance OM.

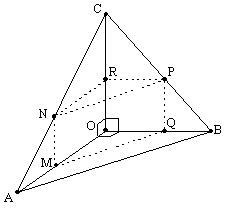A. Section d’aire maximale

1.  Démontrer que MNPQ est un rectangle.
Calculer ses dimensions en fonction de x.

2.  Caractériser la position du point M pour laquelle l’aire du rectangle MNPQ est maximale.

B. Prisme d’aire maximale

1.  Exprimer, en fonction de x, l’aire S(x) du prisme **  OMQRNP.

2.  Démontrer que cette aire admet un maximum.

 

*    On dit que le tétraèdre OABC est trirectangle en O lorsque ses faces OAB, OAC et OBC sont des triangles rectangles en O.

**  On appelle aire du prisme la somme des aires de ses cinq faces.