Pourquoi ce titre ?

Plusieurs approches des nombres premiers sont possibles.

— On peut essayer de trouver les plus grands nombres premiers possibles ; actuellement le plus grand connu a plus de 6. 10⁶ chiffres (c'est un nombre de Mersenne, du type 2ⁿ - 1).

— Prenant un nombre au hasard, on peut se demander s'il est premier. On sait répondre, à ce jour, pour des nombres ayant jusqu'à 500 chiffres.

— On peut enfin se proposer de trouver le n^ième nombre premier ; actuellement le dernier de la liste connu a environ 20 chiffres.

C'est à ce dernier problème que s'intéresse Michel Balazard.

Il s'agit donc du problème de la répartition des nombres premiers dans l'ensemble des entiers naturels. On s'intéresse à la suite (p_n) des nombres premiers ; on a p₁ = 2, p₂ = 3, etc.

Les étapes historiques de cette recherche

Première étape : le mélange des structures

Il s'agit de regarder les entiers à travers les deux structures données par les relations d'ordre sur N : la première par rapport à l'addition a ≤ b si b = a + c, la deuxième par rapport à la multiplication a / b si b = ac.

Deuxième étape : "p_n existe pour tout n"

Le théorème est démontré dans les Éléments d'Euclide.

Dans la démonstration, on utilise : a = p₁ p₂ ... p_N + 1 qui fait bien intervenir le mélange des structures.

Troisième étape

Le théorème fondamental de l'arithmétique sur la décomposition en produit de facteurs premiers et l'identité d'Euler en 1750 qui relie la fonction zêta,

.

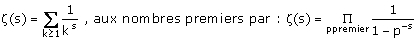Quatrième étape

Un peu avant 1800, Gauss conjecture que la densité des nombres premiers autour de x est en 1 / ln(x), puis Legendre conjecture que le nombre de nombres premiers inférieurs ou égaux à x est à peu près égal à x / ln(x) (l'affirmation est appelée le théorème des nombres premiers).

Cinquième étape

En 1850, Tchebytchev fabrique un système linéaire infini dont les inconnues sont les ln(p) avec p premier, à partir de la décomposition de chaque entier en produit de nombres premiers. Il en déduit une identité qui est cohérente avec ce qu'avaient trouvé Gauss et Legendre.

Sixième étape

Riemann en 1859 énonce une identité qui fait intervenir la fonction ζ,  mais prolongée analytiquement à C - {1}, ainsi que la fonction logarithme intégral. Ce qui nous rapproche de la dernière étape.

Dernière étape

En 1896, Hadamard et De La Vallée-Poussin démontrent le théorème des nombres premiers et donnent une approximation de p_n.

Il semble qu'Erdös ait aussi apporté sa pierre à l'édifice vers 1950.

Actuellement

On peut actuellement trouver les k/2 premiers chiffres de p_n mais les autres fluctuent encore trop !

À travers cet aperçu historique, nous avons pu profiter une nouvelle fois de toute la richesse des mathématiques, de cette construction toujours en mouvement et jamais achevée.