1. Pythagore

Les témoignages sur Pythagore sont presque tous tardifs et douteux. Il serait né vers 580 av J.C. à Samos, île des Sporades ; on fixe sa mort à 497. La légende le décrit comme un thaumaturge, intermédiaire entre les dieux et les hommes. Il fut le fondateur d’une secte d’initiés, dont les dogmes étaient vraisemblablement secrets, à l’origine.

Son enseignement était sans doute principalement de nature religieuse et philosophique ; mais il possédait aussi des aspects mathématique, musical, cosmologique. Aristote, dans sa Métaphysique, insiste sur l’aspect mathématique :

" À l’époque de Leucippe et Démocrite, et même avant eux, ceux qu’on appelle Pythagoriciens s’intéressèrent les premiers aux mathématiques et les firent progresser. Comme ils avaient été élevés dans cette science, ils crurent que ses principes étaient les principes de toutes choses ; et puisque par nature les nombres sont les premiers des principes mathématiques, c’est dans les nombres qu’ils pensaient voir de nombreuses similitudes avec les êtres éternels, ainsi qu’avec les créatures soumises au devenir, bien plus encore que dans le feu, la terre et l’eau. " ( in : Pythagore, Mattei, Que Sais-Je ? )

2. Les nombres entiers

Pour les Pythagoriciens, donc, les entiers et les rapports d’entiers expliquaient le monde, et revêtaient de plus une valeur philosophique, religieuse, sacrée.  

Les quatre premiers nombres, 1, 2, 3 et 4, constituent le triangle sacré de la tétrade ou tétraktys, représentée sous la forme d’un nombre triangulaire. Elle faisait l’objet d’un véritable culte, et était cité dans la célèbre invocation de Pythagore : " Par celui qui a révélé à nos têtes la Tétraktys qui est source et racine de la nature inépuisable ".

Les Pythagoriciens représentaient couramment les nombres par de telles figures.

Nombres triangulaires : 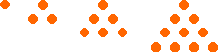   en général 

Nombres rectangles :    etc…n²

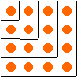	Un nombre carré étant mis sous la forme ci-contre, on voit clairement qu’il est égal à la somme des premiers entiers : 1 + 3 + 5 + … + (2n - 1) = n2.  Sur ces deux figures, on voit apparaître le GNOMON, autrement dit l’équerre, qu’il faut ajouter à un rectangle ou un carré pour obtenir le suivant. Nous reverrons le gnomon chez Euclide.
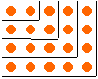	Un nombre comme celui représenté ci-contre s’appelle un nombre rectangulaire. Pour nous, il s’écrit de la forme : n(n - 1). On voit clairement que la somme des premiers nombres pairs donne un nombre rectangulaire : 2 + 4 + 6 + … + 2n = n(n + 1).

Les découvertes mathématiques attribuées à Pythagore par les Grecs, à tort ou à raison, sont innombrables. Par exemple leur propre système de numération. Citons aussi, en arithmétique, les concepts de nombre parfaits, de nombres amicaux, et aussi les triplets de Pythagore.

Ces derniers résolvent le problème suivant :

Quels sont les triangles rectangles que l’on peut construire, dont les mesures des trois côtés sont en nombre entiers ?

Il s’agit donc de trouver des entiers positifs a, b, h, tels que a² + b² = h² .

Exercice pour la classe (seconde)

On cherche les formes de tous les triangles rectangles possibles, dont les mesures des trois longueurs des côtés, en centimètres, soit entières, et dont l’un des côtés de l’angle droit mesure 15 cm.

1) On note h la mesure de l’hypothénuse et a la mesure de l’autre côté de l’angle droit.
Démontrer que (h - d) (h + d) = 15^{2 .}

2) On pose désormais p = h - d et q = h + d. On a donc : pq = 15²  et p < q.

a) On suppose p = 3. Trouver la valeur de q. En déduire les valeurs de h et de d. Tracer le triangle correspondant.

b) Trouver les différents couples (p, q) de nombres entiers tels que pq = 15^{2 et} p < q.En déduire les différentes valeurs possibles de h et d. Tracer dans chaque cas le triangle rectangle correspondant.

Voici des résultats plus élaborés.

Premier théorème

Soit m et n deux entiers de même parité.
On obtient un triplet (a, b, h) de Pythagore en posant : a = m² - n^{2 ;} b = 2mn ; h = m² + n^2.

Évidemment, pour tout k entier, (ka, kb ,kh) est également un triplet de Pythagore.
Il est aisé de faire démontrer aux élèves que ces triplets sont solutions.

Le théorème suivant, que l’on trouve chez Euclide, est plus difficile, mais intéressant, à démontrer :

Deuxième théorème (réciproque)

Les triplets de la forme (k(m² - n^2), k.2mn, k(m² + n²)) sont les seuls triplets de Pythagore^.

3. Les rapports

Tout aussi important pour les Pythagoriciens que les nombres entiers, et issus d’eux : les rapports ou proportions. Nous verrons une utilisation en musique des fractions simples.

La considération de ces différents rapports débouche sur les moyennes ou médiétés
Voici comment Nicomaque présente les différentes moyennes.
(Cité par Mattei, Pythagore et les Pythagoriciens, ouvr. cité).

Soient trois grandeurs a, b, c avec a < b < c. Ces grandeurs sont en :

• Médiété arithmétique si :
  .

Exemple : 4, 5, 6 ou 5, 9, 13.
On dit alors que b est la moyenne arithmétique de a et c.

• Médiété géométrique si :
  .

Exemple : 7, 21, 63 .
On dit alors que b est la moyenne arithmétique de a et c.

• Médiété harmonique si :
  

Exemple : 3, 4, 6 . On dit alors que b est la moyenne harmonique de a et c.
On peut remarquer que cette première relation est équivalente à la suivante :
 .

Autrement dit : trois nombres sont en médiété harmonique si et seulement si leurs inverses sont en médiété arithmétique.

• Autre remarque

Soit a et c deux grandeurs, m leur moyenne arithmétique et h leur moyenne harmonique.
Alors on a l’égalité de proportion suivante :
 .
La vérification de cette relation donne lieu à un calcul littéral assez intéressant.

• La proportion " dorée ", apparue plus tardivement, appartient au même ordre d’idées.

On a proportion dorée entre a et c si : 
.
Ceci équivaut à : 
# 1,618 28….

Les considérations sur les rapports entraînent la nécessité de règles de calcul. Voici les règles du calcul des proportions telles qu’elles étaient exposées au moins jusqu’à la Renaissance. On les trouve par exemple chez Galilée.

Soit a, b, c, d quatre grandeurs, qui étaient généralement des longueurs.
À partir de l’égalité de rapports :
 
on obtient :

• Convertendo, en renversant :
  
• Permutando, en échangeant :
   .
• Componendo, par addition: 
  
• Dividendo, par soustraction:
   

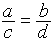Enfin, à partir des égalités :
,
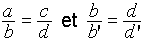nous pouvons conclure d’après la règle ex aequali :
.