que l’on résout aisément.
| Résolutions calculatoires |
| Équipe académique mathématiques Bordeaux, le 5 décembre 1999 |
1. Les Egyptiens
Leur algèbre est élémentaire. Ils appelaient parfois l’inconnue " aha ". Leurs recherches ne pouvaient être que laborieuses, car ils ne disposaient pas du concept général de fraction.
Petit problème égyptien
Une quantité et son 1/7 font 24.
Les Égyptiens ne disposent pas du concept général de fraction. Ils
utilisent donc une méthode de fausse position :
Supposons que cette quantité soit 7, alors le résultat serait 7 + 1/7. 7 = 8.
Or le résultat est le triple de 8 ; c’est donc que la quantité de départ
est le triple de 7, soit 21, qui est la solution.
Ce qui, en tableau, pourrait se présenter ainsi :
| Quantité | 7 | ??? |
| Quantité + septième | 8 | 24 |
| opérateur |
---- x3 ----> |
Petit problème égyptien plus compliqué
Systèmes 2 x 2 ; suites arithmétiques
| 100 pains pour 5 hommes. Le septième de la somme des trois grosses parts est égal à la somme des deux plus petites parts. Quelle est la différence [constante] entre les parts ? |
| Problème n° 40 du Papyrus Rhind, 1650 AV
J.C. Références : Pichot, pages 233/234 ou Dedron-Itard page 303 |
1. Formalisation moderne du problème (niveau collège)
Il faut comprendre que les parts forment une suite arithmétique.
Soit donc p la première part, et d la différence entre une part et la suivante (la raison de la suite), les différentes parts sont : p, p + r, p + 2r, p + 3r, p + 4r
On aboutit donc au système :
![]()
que l’on résout aisément.
2. Solution Égyptienne
La chose comme elle se produit. [Suppose que] la différence des parts est 5 1/2:
|
1 |
6 1/2 |
12 |
17 1/2 |
23 |
total 60 |
Il faut multiplier 60 par 1 2/3 pour obtenir 100 (calcul annexe).
Multiplie par 1 2/3 :
1 devient 1 2/3
6 1/2 devient 10 2/3 1/6
12 devient 20
17 1/2 devient 29 1/6
23 devient 38 1/3
[ Sous-entendu : avec une différence constante de 9 1/6]
3. Analyse moderne de la solution égyptienne
C’est évidemment une méthode de fausse position, en l’absence de notations littérales.Le premier calcul, qui aboutit à la raison 5 1/2 pour une première part de 1, n’est pas expliqué par le texte.
Toute la méthode repose sur le fait que la seconde condition (la seconde équation du système) est linéaire, sans second membre. Donc, si (p’, r’) en est solution, il en ira de même de (k.p’ , k.r’ ). Le scribe cherche donc la raison r’ telle que (1, r’) vérifie la seconde condition. Il trouve r’ = 5 1/2, mais n’explique pas sa démarche. Il multiplie ces deux nombres par k pour ajuster la première condition, affine : alors le couple (k.1, k.r’) sera solution du système.
Dans le même style
| Dix frères se sont partagés une mine deux-tiers
d’argent. Chaque frère s’est élevé au-dessus de l’autre.
[toujours de la même quantité d’argent] De combien, je ne sais. La
part du huitième est de 6 sicles. De combien un frère s’est-il élevé
au-dessus de l’autre ? [une mine fait 60 sicles ] |
| Références : Pichot, pages 90/91 ou Dedron-Itard page 304 STR 362, 1ère dynastie babylonienne. |
Les Babyloniens, y compris ceux de la dynastie d’Hammourabi, vers 1800-1600 avant Jésus-Christ, étaient de grands algébristes. D’après Otto Neugebauer, " On a affaire à un niveau de développement remarquable, comparable, par de nombreux aspects, à celui du début de la Renaissance " . L’algèbre babylonienne repose sur la puissance de leur système sexagésimal.
![]()
Une petite tablette d’argile babylonienne, reproduite dans
l’ouvrage cité de Neugebauer, représente un carré, 30 pour le côté, et
pour la diagonale, en sexagésimal : 42, 25, 35 .
Elle founit aussi leur quotient 1 ; 24, 51, 10, soit, en décimal 1,414
212 963, au lieu d’environ 1,414 213 562, ce qui donne une erreur d’environ
6. 10-7.
Pas si mal !
Les Babyloniens étaient experts dans les problèmes de degré 2. D’après Neugebauer, ils ont inspiré tout l’aspect " algébrique " d’Euclide et de Diophante.
Ils se ramenaient en général à la forme normale du degré 2, à savoir
![]()
qu’ils traitaient de la façon suivante (attention : uniquement sur des
exemples individuels numériques):
Posons :
![]() ,
,
puis x = m + d, y = m - d.
Le système devient alors : m2 - d2 = p ; d’où : d2 = p + m2 ; d’où la valeur de d grâce aux tables de racines carrées ou de carrés ; d’où x et y.
Mais les Babyloniens s’intéressaient aussi aux puissances successives d’un nombre donné, aux intérêts composés, à certaines équations exponentielles de la forme ax = b.
On a trouvé chez eux l’équivalent des formules suivantes
: 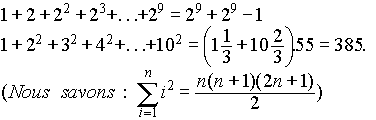
D’après Neugebauer, la seule limite à la virtuosité technique
des Babyloniens était dans leur manque de notations algébriques générales
; de plus, on ne pourrait pas dire qu’ils ont fondé une science mathématique
abstraite, car leur calcul n’utilise ni la déduction, ni le concept
général . Par exemple, ils ne se posent pas la question du statut du nombre,
ni, par exemple, celui de l’irrationnalité de ![]() .
.