Exercice n°1

Exercice n°2

1) La valeur maximale est atteinte lorsque R est en B, soit x = 4.

La valeur minimale sera atteinte lorsque T sera en D.

.

On note I l’intervalle obtenu.

2) Soit H le projeté orthogonal de S sur (AD).

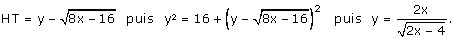
3) Soit S(x) l’aire de la partie repliée.

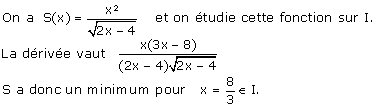
On vérifie alors que le triangle AST est équilatéral.

Exercice 3

A)     Il y a bien sûr la solution x = y = z = 0. Sinon, les trois entiers sont différents de 0.

Soit x le plus grand des trois. On a x y z £ 3 x puis y z £ 3 ce qui ne laisse que trois cas à étudier.

Seule la solution 1, 2, 3 convient.

B) 1) On remarque d’abord qu’au plus un des trois nombres vaut 1 et qu’ils sont tous non nuls. Supposons y ¹ 1, z ¹ 1 et supposons que y est le plus grand des 3 nombres.

x (y z – 1) = y + z + n donne y z – 1  £ y + z + n

soit y z + 1 – y – z £ n + 2

soit (y – 1) (z – 1) £ n + 2 et finalement y £ n + 3.

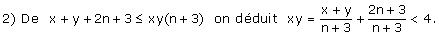
Seule la solution  x = 1,  y = 2 convient.

3) Pour n = 1, aucune solution.

Pour n = 2, la solution x = y = z = 2  convient.

Exercice 4

1) a) Si b = c, MNC est isocèle et p = b est la seule possibilité.

b) Si b>c, on pose x = BM et par Thalès on trouve :

2) On porte p et c sur [AC] en partant de A, on obtient D et E.

On  trace la parallèle à (BE) passant par D, elle coupe [BC] en M.