Olympiades académiques de mathématiques 2004
Sujet
Antenne communication
Bordeaux, le 24 mars 2004

Sujet  Solutions  Palmarès  Prix

 

24/03/2004
Classe de première
Durée : 4 heures.
Les quatre exercices sont indépendants. Les calculatrices sont autorisées.

 

Exercice 1

On définit pour chaque couple de réels (a, b) la fonction f par :

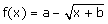
Deux nombres réels u et v distincts sont dits échangeables s’il existe au moins un couple de réels (a, b) tel que la fonction f vérifie à la fois f(u) = v et f(v) = u.

1°) Montrer que 2 et 3 sont échangeables.

2°) Peut on en dire autant de 4 et 7 ?

3°) A quelle condition deux entiers u et v sont ils échangeables ?

 

Exercice 2

Soit ABCD une feuille de papier rectangulaire de largeur
AB = 4 et de longueur BC = 6. Soit R un point de [AB] (bord inférieur de la feuille) et T un point de [AD] (bord droit de la feuille). On replie la feuille suivant le segment [RT] et on appelle S la nouvelle position de point A (coin inférieur droit de la feuille).

Voir figure ci contre.

Dans tout l’exercice on s’intéresse au cas où S est sur le segment [BC] (bord gauche de la feuille).

On pose AR = x et AT = y.

1°)   Trouver les valeurs minimale et maximale de x.

2°)   Trouver une relation entre x et y lorsque S se déplace sur [BC].

3°)   Trouver la valeur de x pour laquelle l’aire de la partie repliée (triangle SRT) est minimale. Quelle est alors la nature du triangle AST ?

 

Exercice 3

Partie A

Déterminer tous les entiers naturels x, y, z vérifiant l’équation : x + y + z = xyz

Partie B

Pour n entier naturel non nul donné, on s’intéresse aux entiers naturels x, y et z vérifiant l’équation : x + y + z + n = xyz.

1°) Montrer que les nombres x, y et z sont tous inférieurs ou égaux à n + 3.

2°) On suppose que z = n + 3. Déterminer les valeurs possibles de x et y.

3°) Quelle est la plus petite valeur de n pour laquelle on peut trouver des entiers naturels

x, y, z strictement inférieurs à n + 3, vérifiant x + y + z + n = xyz ?

 

Exercice 4

Un segment de longueur p (p > 0) étant donné, on cherche à construire un parallélogramme ANMP ayant pour périmètre 2p, comme indiqué sur la figure ci-dessous, M, N et P appartenant chacun à l’un des côtés du triangle.

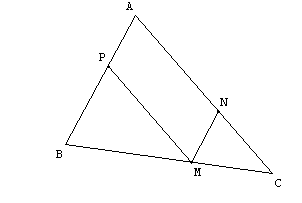
On note a la longueur du côté [BC], b celle du côté [AC] et c celle du côté [AB].

On suppose b >= c.

1°) Discuter suivant les valeurs de p l’existence d’un tel parallélogramme

– lorsque b = c

- lorsque b > c.

2°) Proposer, lorsque le problème a une solution, une construction du parallélogramme à la règle non graduée et au compas.