| Olympiades académiques de mathématiques 2005 Une solution |
| Antenne communication Bordeaux, le 30 mars 2005 |
| Sujet Solutions Palmarès Prix Palmarès national |
Exercice 1

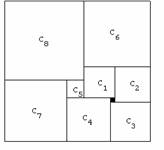
Pour résoudre cet exercice, il faut partir d’un des carrés jouxtant le carré unité (en noir sur la figure) et de préférence commencer par le plus petit (carré C1).
Si ce carré C1 a pour côté c, le carré C2 a pour côté c + 1 et le carré C3 a pour côté c + 2.
Le carré C4 a pour côté c + 3.
(À chaque fois, on utilise le fait que le carré noir a pour côté 1)
Ceci permet de déduire que le carré C5 pour côté 4.
Quant au carré C6 il a pour côté 2c + 1.
On obtient qu’une des dimensions du rectangle initial est :
(2c + 1) + (c + 1) + (c + 2) = 4c + 4.
Le carré C7 a pour côté c + 3 + 4 = c + 7. Donc l’autre dimension du rectangle initial est :
(c + 7) + (c + 3) + (c + 2) = 3c +12.
Le dernier carré C8 a pour côté c + 7 + 4 =c + 11.
Finalement deux côtés opposés du rectangle ont pour dimensions :
4c + 4 et (c + 7) + (c + 11) = 2c + 18
Les deux côtés étant de même longueur, on a 4c + 4 = 2c + 18 ce qui donne c = 7.
En conclusion, le rectangle initial a pour dimensions 32u et 33u.
Exercice 2
1.C’est une application de l’inégalité triangulaire.
2.On obtient une longueur totale de 0.5 + rac(5), ce qui est inférieur à 2 rac(2) de la question 1.
3. Pour cette question, on exprime la longueur en fonction de x. On obtient
![]()
Si on trace la courbe représentative de cette fonction sur l’intervalle
[0 ; 1] avec la calculatrice, on constate qu’il y a un minimum d’environ
2.732 atteint pour x environ égal à 0.4226. On retrouve ce résultat en dérivant
la fonction obtenue, on a alors la valeur exacte de x pour laquelle le minimum
est atteint et c’est ![]() .
.
Exercice 3
La première question est un exercice classique de seconde :
Si on note I le centre du cercle inscrit du triangle ABC, le triangle IAB a pour aire (r×AB)/2, le triangle IBC a pour aire (r×BC)/2 et le triangle IAC a pour aire (r×AC)/2, la somme de ces trois aires est l’aire de ABC et on trouve bien le résultat.
Dans la deuxième question, le 1) se résout en utilisant Thalès et la propriété obtenue dans la première question ; le plus simple est de noter K le projeté orthogonal de I sur [AC] ; on a S = r ×p / 2 et ici p = 3x+3 = 3 AC. D’autre part, on a aussi S = BH ×AC /2
donc BH = 3 r = 3 IK ;
Puis avec Thalès, on obtient ID/BD = IK/BH = 1/3, d’où le résultat.
Pour le 2), on aboutit à une équation du second degré, x² - 2x – 3 = 0 en utilisant Pythagore, d’où la solution x = 3. Les côtés du triangle sont alors de 3, 4 et 5.
Pour le 3), on trouve le résultat en utilisant la formule d’Al Kaschi mais on peut aussi obtenir une partie des résultats par des considérations géométriques.
Exercice 4
Le lièvre se déplace 363 fois plus vite que la tortue. Lorsque la tortue a parcouru une moitié du circuit, le lièvre a parcouru, lui, 363 moitiés de circuit, c'est-à-dire 181 « tours complets » et un demi circuit, à l’issue duquel les deux animaux se croisent. Le lièvre a donc dépassé 181 fois la tortue (à chaque passage sur une boucle de rang pair de son parcours), et l’a croisée une fois au carrefour : ce premier demi circuit de la tortue génère donc 182 « dépassements ou croisements ». Au second demi circuit effectué par la tortue, le même raisonnement s’applique (la position initiale étant comptabilisée dans le décompte précédent), et ainsi de suite. Ainsi, chaque demi circuit effectué par la tortue génère 182 rencontres, dont 181 dépassements et un seul croisement à la fin.
2005 = 11 x 182 + 3
Donc pour 2005 « croisements ou dépassements », la tortue aura parcouru 11 moitiés de circuit, qui auront généré 11 croisements.