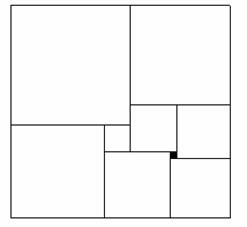
Le rectangle ci-contre est pavé par neuf carrés. Le carré noir a pour côté une unité.
Quelles sont les dimensions du rectangle ?
| Olympiades académiques de mathématiques 2005 Sujet |
| Antenne communication Bordeaux, le 23 mars 2005 |
| Sujet Solutions Palmarès Prix Palmarès national |
Classe de Première
Durée : 4 heures
Les quatre exercices sont indépendants.
Les calculatrices sont autorisées.
Exercice 1 - Un pavage
| Le rectangle ci-contre est pavé par neuf carrés. Le carré noir a pour côté une unité. Quelles sont les dimensions du rectangle ? |
 |
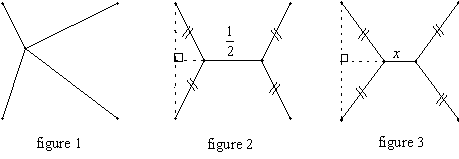
Exercice 2 - Le plus court réseau routier
Quatre maisons sont situées aux quatre coins d’un carré de côté 1. On souhaite construire un réseau routier qui permet de relier les maisons mais on veut que ce réseau soit le plus court possible.
1. Dans un premier temps, on envisage de créer un rond point à l’intérieur du carré comme dessiné sur la figure 1. Démontrer que dans ce cas, le réseau le plus court est obtenu lorsque le rond point est situé au centre du carré.
2. Un des habitants s’est rendu compte qu’avec deux ronds points placés comme sur la figure 2, on pouvait réduire la longueur du réseau.Vérifier qu’il a raison.
3. Trouver la valeur de x qui permet d’obtenir le réseau le plus court dans la configuration de la figure 3.
Exercice 3 - Les triangles académiques
Première question
Démontrer que dans un triangle ABC, si on note p le périmètre et r le rayon du cercle inscrit, alors l’aire S du triangle est donnée par :
![]() .
.
Deuxième question
Une unité de longueur étant choisie, on appelle triangle académique un triangle dont les mesures des côtés sont en progression arithmétique de raison 1.
Dans tout l’exercice, on considère un triangle ABC tel que AB < AC < BC.
Ainsi, un tel triangle est académique si : AC = AB + 1 et BC = AB + 2.
| 1. On note I le centre
du cercle inscrit dans le triangle ABC et D le pied de la bissectrice
intérieure de l’angle Démontrer que si ABC est académique alors BD = 3ID.
2. Un triangle académique peut-il être rectangle ? Justifier. Quelles sont alors ses dimensions ?
3. On suppose que le triangle ABC est académique et que AB > 3. Démontrer que les trois angles du triangle ABC sont aigus et qu’un seul d’entre eux a une mesure supérieure à 60°.
|
|
Exercice 4 - Le lièvre et la tortue
La piste du champiodrome a la forme suivante : deux arcs formant les trois quarts d’un cercle, raccordés par les deux diagonales d’un carré, ces deux diagonales se coupant en un carrefour.
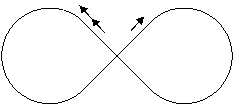
Au même instant, une tortue et un lièvre partent du carrefour, empruntant deux diagonales différentes menant à deux arcs de cercle différents (sur le dessin, une flèche pour la tortue, deux flèches pour le lièvre).
Les deux animaux courent à vitesse constante, et la tortue met 363 secondes pour parcourir la distance parcourue par le lièvre en 1 seconde.
Après 2005 rencontres (dépassements sur la piste ou croisements au carrefour) hormis le départ, le lièvre abandonne.
Combien de fois avait-il croisé la tortue au carrefour ?