Corrigé des exercices de la première série.

Rappel des énoncés

Exercice 1

À l’étage de rang p, le nombre de boîtes est mn.
À l’étage en dessous, de rang p - 1, le nombre de boîtes est (m + 1)(n + 1)
À l’étage en dessous, de rang p - 2, le nombre de boîtes est (m + 2)(n + 2)
…….
À l’étage du bas, de rang 1, c’est à dire [p - (p - 1)], le nombre de boîtes est (m + p - 1)(n + p - 1)

Le nombre total de boîtes,S, est donc, pour p étapes :
S = mn + (m + 1)(n + 1) + (m + 2)(n + 2) + ….. + (m + p - 1)(n + p - 1)
   = mn + mn + m + n + 1 + mn + 2m + 2n + 4 + ….. + mn + (p - 1)m + (p - 1)n + (p - 1)²
   = p(mn) + m (1 + 2 + …. + p - 1) + n (1 + 2 + … + p - 1) + 1 + 4 + … + (p - 1)²
   = mnp + (m + n) [p(p - 1)/2] + [(p - 1)p(2p - 1)/6]

Pour mn = 6 , il y a deux possibilités :

– l’un des facteurs est 1 et l’autre 6 alors S = 3220, et p = 20
– l’un des facteurs est 3 et l’autre 2 alors S = 3040

Exercice 2

On note A,B,C et D les sommets du toit rectangulaire, T la cime du mât et H le point de contact du mat avec le toit.
Soit h la hauteur du mât et x la longueur du cable restant.

Le mât étant perpendiculaire au plan du toit, les triangles TAH,TBH,TCH et TDH sont rectangles.
Donc d’après Pythagore, on a : AH² = 49 - h² , BH² = 1 - h² , CH² = 16 - h² et DH² = x² - h².

On note ensuite U,V,X et Y les projetés orthogonaux respectifs de H sur les côtés [AB], [BC], [CD] et [DA].
On a encore des triangles rectangles et on obtient :
DH² + BH² = (DX² + XH²) + (BV² + HV²)
 = AU² + CV² + UH² + HV² = AU² + UH² + CV² + HV² = AH² + CH²
d’où x² - h² + 1 - h² = 49 - h² + 4 - h² ce qui donne x = 8.

Exercice 3

Si les sommets sont sur des intersections de quadrillage, le carré du côté a du triangle équilatéral est un entier ( par Pythagore)et l’aire est alors :
.
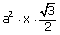C’est un irrationnel.

Or, si les sommets sont sur des intersections de quadrillage, on peut obtenir l’aire du triangle en le mettant dans un rectangle à côtés entiers et en faisant :

aire du rectangle – aire des trois triangles rectangles qui entourent le triangle équilatéral,

Mais dans ce cas on obtient un nombre décimal pour l’aire ce qui est en contradiction avec le calcul précédent.

Conclusion : on ne peut pas construire un tel triangle équilatéral.
Pour l’hexagone régulier on se ramène au cas précédent puisqu’il est constitué de 6 triangles équilatéraux.
Pour le pentagone on peut commencer par étudier le cas d’un triangle isocèle dont l’angle au sommet mesure 72°
() .

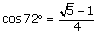Exercice 4

Pour l'Exercice IV, il y a deux cas à considerer:

1° cas: (AB) et (CD) sont sécantes en O; on considère alors la symétrie d'axe la bissectrice intérieure de l'angle AOD, on note D1 et C1 les images de D et C par la symétrie et on montre rapidement le résultat par homothétie ( ou triangles semblables) de centre O.

2° cas: (AB) // (BC) , alors on prend la symétrie orthogonale qui transforme (AB) en (CD) et on a encore plus vite le résultat .

Exercice 5

La réponse est oui.

En effet, si on prend deux régions ayant un bord commun, notons les R et R’, notons a le nombre de cercles qui contiennent R et a’ le nombre de cercles qui contiennent R’ alors a est pair et a’ est impair ou le contraire. Donc, en coloriant d’une couleur les régions contenues dans un nombre pair de cercle et d’une autre couleur les autres, on aura bien les conditions demandées.

Exercice 6

On note c la longueur AB, b la longueur AC et a la longueur BC.

On a 0 < x < b . Dans MAB rectangle en A on a MB² = c² + x²
La relation MB² = AC x MC (il y avait une erreur dans le texte) s’écrit : c² + x² = b (b - x)
soit x² + bx + c² - b² = 0

1) Cas particuliers

b/c = 2  donne x = - 3c ou x = c avec 0<x<2c donc une solution qui correspond à M milieu de [AC] .

b/c = 1 donne x² + bx = 0 donc pas de solution.

2) Cas général

b/c = k , l’équation devient x² + kcx + c² - k²c² = 0 et 0 < x < k c

D = c² (5k² - 4) d’où : si 0 < k < , Δ < 0 donc pas de solution.

Si k = , il y a une solution mais elle est négative donc le problème n’a pas de solution dans ce cas.

Si k >  , l’équation a deux solutions dont l’une est négative, donc la seule solution possible est
.

Il reste la condition 0 < x < k c

La condition x > 0, donne k > 1 et la condition x < k c est toujours vérifiée.

Conclusion : le problème a une solution pour k > 1.

Exercice 7

Soit R le rayon de l’astéroïde , A le point de départ sur l’équateur, B le point atteint au bout de 100 km vers le nord, C le point atteint au bout de 100 km vers l’est  et D le point atteint au bout de 100 km vers le sud.

Le rayon du parallèle passant par B et C est égal à R/2, car la distance BC est la moitié de la distance AD. Si on note a une mesure de l’angle AOB, avec O centre de la sphère, on a alors cos a = ½ donc a = p/3. On en déduit que R = 300/p. La distance qu’il doit parcourir est donc
D = 2pR – 200 soit D = 400 km .

Exercice 8

Si k polygones réguliers ayant n côtés se raccordent au même sommet commun, on a k a = 2 p où a est l’angle du polygone.

Or l’angle d’un polygone à n côtés est a = p (n - 2)/n.
En effet, le polygone régulier est formé de n triangles isocèles d’angle au sommet 2 p /n donc les angles à la base mesurent p /2 – p /n et a est égal au double des angles à la base d’où le résultat.
On a donc k ((n - 2) / n)) p = 2 p soit k (n - 2) = 2 n où n et k sont des entiers supérieurs à 2.
La relation peut s’écrire aussi :
.

On voit déjà que si k et n sont trop grands, leurs inverses seront trop petits pour que la somme fasse 0,5 ; plus précisément, on a :

• pour k = 3 ,on obtient n = 6 (hexagone régulier) ;
• pour k = 4, on obtient n = 4 ( carré) ;
• pour k = 5, on obtient n = 10/3, impossible ;
• pour k = 6, on obtient n = 3 (triangle équilatéral).
• Enfin, si k > 6 alors 1/k < 1/6 , donc 1/n > 1/2 –1/6,d’où 1/n >1/3 et n < 3 ce qui est impossible.

Conclusion : si on veut paver le plan avec des polygones réguliers, on ne peut le faire qu’avec des hexagones réguliers, des carrés ou des triangles équilatéraux.

Exercice 9

Notons Q, R, T et U les centres des 4 sphères. Ces 4 points forment un carré.
Notons V son centre. Appelons P le centre de la 5^ième sphère et S le milieu de [QR] , c’est à dire le point de contact de 2 sphères .

Le triangle PQR est équilatéral et PS en est une hauteur, le côté du triangle est 20 cm donc
PS =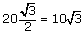 

D’autre part, le triangle PSV est rectangle en V ,on a donc : PV² = PS² - SV² d’où PV² = 200
On a donc PV =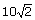 

Enfin, puisque le point V est à 10 cm au dessus de la table, le point P, centre de la 5^ième sphère est situé à une hauteur de cm au dessus de la table.

Exercice 10

Soit L le point d’intersection de [BC] et de la perpendiculaire à [BC] passant par I.

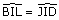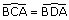On a  , angles opposés par le sommet, , angles inscrits interceptant le même arc, et 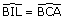, angles à côtés perpendiculaires.
On en déduit que : 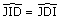, donc le triangle JDI est isocèle en J et JI = JD.
On a de même : 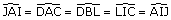, et donc AJI est isocèle en J d’où JA = JI.

On a donc JD = JA et J est le milieu de [AD].

Exercice 11

On démontre d’abord que, si on considère une pièce fixe de centre A et une pièce qui roule sur le bord exterieur de la pièce fixe, l’angle de rotation de cette pièce, quand son centre passe de la position B à la position B’, est 2 a où a est l’angle BAB’ .

Soient O₁, O₂ … O₆ les centres des 6 pièces. Ces centres forment un hexagone régulier.

Soit A_ij le centre de la septième pièce quand elle touche les pièces consécutives ayant O_i et O_j pour centres. L’angle de la rotation sur elle même de la septième pièce entre la moment où elle touche les pièces ayant O_i et O_j pour centre et le moment où elle touche les pièces suivantes ayant O_j et O_k pour centre est égal, d’après ce qui précède, à 2 x angle(A_ij O_j A_jk) = 2 x a_j .

Alors, si on note t l’angle de rotation sur elle même de la septième pièce quand elle a repris sa position initiale, on a : t = 2 x (a₁ + a₂ + a₃ + a₄ + a₅ + a₆).

Les triangles O_iO_jA_ij sont équilatéraux et la somme des angles d’un hexagone est 720° donc  les a_i sont égaux à 120° et t = 12 x 120° = 4 x 360°. La septième pièce fera donc 4 rotations sur elle même.