| Exercices de préparation aux Olympiades (deuxième série) |
| Exercices proposés par A.Ouardini (collège Val de Saye - St Yzan de Soudiac, Gironde) et posés lors d'olympiades étrangères Bordeaux, le 29 janvier 2004 |
Voici une deuxième série de préparation aux Olympiades de mathématiques, avec des indications de résolution.
![]()
Exercice 1
Soit trois cercles de même rayon ayant un point commun O et qui sont tous trois intérieurs à un triangle ABC de telle sorte que chaque cercle est tangent à deux des côtés du triangle.
Démontrer que les centres des cercles inscrit et circonscrit du triangle ABC et le point O sont alignés. (Olympiades Internationales de Mathématiques 1981)
![]()
Exercice 2
A et B sont deux points tels que AB = 1.
Déterminer tous les points P de la droite (AB) tels que :
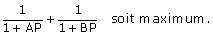
(Olympiades hongroises)
![]()
Exercice 3

(Olympiades roumaines)
![]()
Exercice 4
Déterminer toutes les fonctions numériques f définies sur R vérifiant :
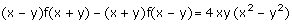
(Olympiades de Singapour)
![]()
Exercice 5
Soient x, y et z trois entiers naturels non nuls, distincts deux à deux.
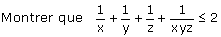
Dans quels cas l’égalité a-t-elle lieu ? (Proposé par A. Ouardini)
![]()