| Exercices de préparation aux Olympiades (deuxième série) |
| Exercices proposés par A.Ouardini (collège Val de Saye - St Yzan de Soudiac, Gironde) et posés lors d'olympiades étrangères Bordeaux, le 29 janvier 2004 |
Indications pour résoudre la deuxième série d'exercices de préparation aux Olympiades de mathématiques.
![]()
Exercice 1
Désigner par O1, O2 et O3 les centres des cercles et remarquer que :
- OO1 = OO2 = OO3 donc O est le
centre du cercle passant par les
trois points O1, O2 et O3.
- (AO1), (BO2) et (CO3) sont les
bissectrices 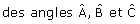 .
.
- donc le centre du cercle inscrit au triangle ABC est le centre de l’homothétie qui transforme respectivement O1, O2, O3 en A, B, C.
![]()
Exercice 2
Poser x = AP ; le problème se ramène à maximiser une fonction réelle.
![]()
Exercice 3
En appliquant le théorème d’Al Kashi, il vient : a² =
b² + c² - bc et on remarque que 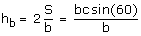
![]()
Exercice 4
On obtient des résultats en posant x + y = t et x – y = t’.
![]()
Exercice 5
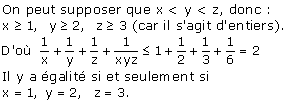
![]()