Voici une troisième série de préparation aux Olympiades de mathématiques, avec des indications de résolution.

Voir les indications.

Problème 1

Considérons un échiquier de 8 x 8 cases et découpons le en p rectangles, en respectant les cases. Le découpage satisfait aux conditions suivantes :

1. Chaque rectangle est formé d’autant de cases blanches que de cases noires.

2. Si a_i est le nombre de cases blanches du i-ième rectangle, alors a₁ < a₂ < … < a_p .

Déterminer la valeur maximale de p pour laquelle un tel découpage est possible.

Indiquer pour cette valeur de p toutes les suites a₁, a₂, ……, a_p possibles.

(Olympiades internationales de Mathématiques 1974)

Problème 2

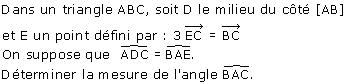
(Olympiades Britanniques)

Problème 3

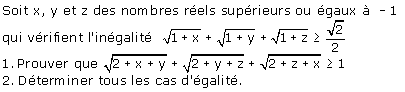
(A. Ouardini)

Problème 4

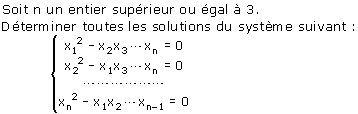
(Olympiades de Croatie)

Problème 5

Soit (a_n) , n ∈  N, une suite réelle strictement croissante qui vérifie : a₀ = 1, et , pour tout n de N, 4a_na_n+1 = ( a_n + a_n+1 – 1)².

Exprimer a_n en fonction de n.

(Olympiades de Hong Kong)

Problème 6

Soit un triangle ABC et un point P à l’intérieur de ce triangle tel que .

Les perpendiculaires à (BC) et (CA) passant par P coupent respectivement ces deux droites aux points L et M. Soit D le milieu de [AB].

Montrer que DL = DM.

(Proposé aux olympiades internationales par la Grande Bretagne en 1982)

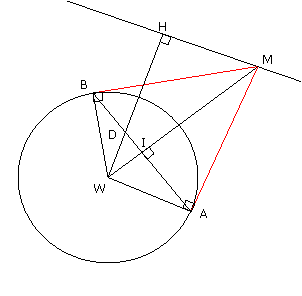
Problème 7

Dans le plan, on considère un cercle (C) et une droite (D) qui ne coupe pas (C).

Par un point M de (D), on mène les deux tangentes (MA) et (MB) à (C) (A et B étant les points contacts).

Quel est le lieu géométrique du milieu de [AB] quand le point M décrit la droite (D) ?

(A. Ouardini)