| Exercices de préparation aux Olympiades (troisième série) |
| Exercices proposés par Abder Ouardini (lycée de la Mer- Gujan-Mestras) ou posés lors d'olympiades étrangères Bordeaux, le 8 mars 2005 |
Indications pour résoudre la troisième série d'exercices de préparation aux Olympiades de mathématiques.
Problème 1
On a : a1 < a2 < … < ap avec a1 ≥ 1 donc k ≤ ak pour tout k.
Donc a1 + a2 + … + ap ≥ 1 + 2 + … + p = p(p+1)/2.
Donc p(p+1)/2 ≤ 32 (il y a 32 cases blanches).
Donc la valeur maximale de p est 7.
D’autre part, a1 + a2 + … + a6 ≥ 6×7/2 = 21, donc 32 – a7 ≥ 21, d’où a7 ≤ 11.
Donc a7 = 7, 8, 9, 10, 11 …
Pour a7 = 7, il n’y a aucune solution.
Les 4 possibilités sont :
1 + 2 + 3 + 5 + 6 + 7 + 8
1 + 2 + 3 + 4 + 5 + 8 + 9
1 + 2 + 3 + 4 + 6 + 7 + 9
1 + 2 + 3 + 4 + 5 + 7 + 10
Problème 2
Soit G le point d’intersection de (CD) et (AE), et F sur [BC] tel que BF = FE = EC.
On a (DF) // (AE) donc G est le milieu de [DC].
Le triangle ADG est isocèle en G par hypothèse donc DG = GC = GA.
Le triangle ADC est donc rectangle en A et, par suite,
![]()
Problème 3
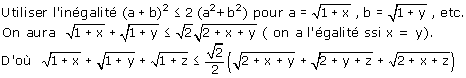
Problème 4
On a :
x1² = x2 x3 …..xn
x2² = x1x3 …..xn
………………..
xn² = x1x2…….xn-1
Par produit membre à membre on obtient : (x1x2……xn)² = (x1x2……xn) n-1
1° cas : x1x2……xn = 0
Il existe alors j tel que xj = 0. Donc x1 = x2 = … = xn = 0
2° cas : n pair
On a x1x2 … xn = 1.
Donc pour tout j, xj 3 = x1x2 … xn = 1
Par suite x1 = x2 = … = xn = 1
3° cas : n impair différent de 3
On a x1x2……xn = ± 1.
Donc pour tout j, xj 3 = ± 1, donc pour tout j, xj = ± 1.
4° cas : n = 3
x1² = x2x3
x2² = x1x3
x3² = x1x2
Posons x1x2x3 = a3, a réel.
Si a = 0, alors x1 = x2 = x3 = 0
Si a ≠ 0, alors pour tout j, xj 3 = a3,donc xj = a.
Problème 5
Problème 6
L’astuce consiste à définir I milieu de [AP] et J milieu de [BP].
On montre alors que les triangles MID et LJD sont isométriques en utilisant le fait que IDJP est un parallélogramme.
Problème 7