Probabilités

 

      Un exemple d’introduction de la loi normale aux élèves

 

Pré-requis

• Intégration
• Notion de densité : définition, propriétés, lois usuelles
• Etude de la fonction  
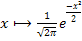   (parité, variations, courbe, estimation de l’aire sous la courbe avec un algorithme qui encadre l’intégrale et/ou avec du calcul formel )

 

Problème concret d'introduction « activité réalisée par les élèves »

• Réactivation de la loi binomiale, représentations graphiques par des diagrammes en bâtons
• Inconvénient du calcul cumulatif si n  est grand en termes de temps et de capacité de la machine

 

Introduction de la loi normale centrée réduite « activité réalisée par le prof devant les élèves  »

•  Conforter les élèves dans les observations de l’activité en faisant varier n et p pour découvrir un invariant : la forme générale du diagramme en bâtons en particulier quand n  augmente, à p  constant
•  Passage du diagramme en bâtons ( suit la loi binomiale B (n;p)) à un histogramme afin d’obtenir des probabilités représentées par des aires : l’idée  étant d’approcher l’aire de rectangles consécutifs par une aire sous une courbe (en cloche) afin d’éviter la sommation
  Sur ce graphique, la largeur des rectangles étant de 1, leur aire est égale à leur hauteur qui est la même que celle des bâtons initiaux. L’amplitude du graphique est augmentée de 0,5 de chaque côté.

 

•  Centrage
1. Observation d’une certaine symétrie dans la représentation graphique autour de la moyenne (l’espérance de la loi binomiale 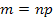  qui elle-même varie avec 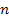 et
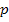
2. Idée de translater la représentation graphique afin de la centrer autour d’un point fixe, le plus naturel étant .
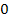3. On s’intéresse alors à la nouvelle variable 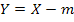avec 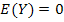 (indépendant d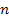e  et de 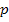) et 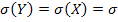 (écart type de la loi binomiale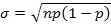

 

•  Réduction
1. On refait varier n à p fixé pour la nouvelle variable Y  : le centrage demeure mais la hauteur des rectangles et l’amplitude du graphique varient  encore de manière significative
2. Questions : comment pourrait-on essayer de limiter ces variations ? Quels sont les paramètres qui les influencent et de quelle manière ?
3. On a réussi à définir une variable Y dont la moyenne ne dépend plus de n  et de p
4. Dans le même ordre d’idée, on peut se demander ce que produirait une action sur l’écart type , d’où l’idée de comparer les graphiques (centrés) dans différents cas :

    écarts types différents

    écarts types identiques ( n petit - grand )

5. On remarque que lorsque l’écart-type est le même, les graphiques se superposent quasiment d’autant plus que n  est grand
6. L’idée est maintenant de trouver une nouvelle variable aléatoire dont l’écart-type ne dépendrait plus de 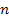 et de > 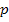comme pour la moyenne
7. Avec la translation, on avait
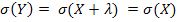
8. On peut faire remarquer aux élèves que 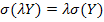 (démontré en 1^ère S)
9. D’où l’idée de prendre 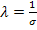 et de poser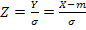  
10. Attention, pour que l’aire des rectangles représentent toujours la probabilité, les largeurs des rectangles étant multipliées par λ 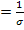 , les hauteurs, doivent, elles, être multipliées par
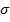
11. On a alors 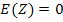 et
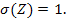
12. On refait varier 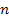 à 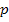 fixé pour la nouvelle variable 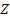: les rectangles bougent légèrement mais l’aire semble rester sensiblement  la même (en particulier quand 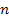 est grand)

 

•  Lien avec la loi normale centrée réduite
  1. Rappel de l’objectif : trouver une courbe permettant d’approcher le calcul de l’aire de rectangles consécutifs de l’histogramme
  2. Observer que l’allure générale de l’histogramme correspondant à la variable Z (forme en cloche) rappelle une courbe déjà étudiée
  3. Tracé de cette courbe sur le même graphique à des fins de comparaisons
  4. Comparaisons sur le graphique de l’aire sous la courbe et sous l’histogramme entre deux bornes données
  5. Généralisation (admis)

 

      Un exemple d’application de la loi normale

 

Echantillonnage :

      Intervalle de fluctuation-Intervalle de confiance

 

Tableau récapitulatif par niveaux

 

 

      Modalités de prise de décision : quelques précautions…

 

•  Lorsque, dans une population, on connaît la proportion p théorique d’un certain caractère, et qu’on regarde, dans un échantillon de taille n, la fréquence d’apparition de ce caractère, il y a alors deux cas possibles :

      La fréquence  de cet échantillon, n’appartient pas à l’intervalle de fluctuation au seuil , et on rejette alors l’hypothèse que cet échantillon soit à l’image de la population avec un risque d’erreur de . Il est alors prudent de rechercher d’autres causes (extérieures) à ce phénomène que le simple « hasard ».

      La fréquence  de cet échantillon, appartient à l’intervalle de fluctuation au seuil , et alors,  on ne peut pas rejeter l’hypothèse que cet échantillon soit à l’image de la population. Dans ce cas, l’échantillon est accepté mais sans argument mathématique réel (juste parce ce qu’on n’a pas trouvé de raison de le rejeter).

 

Remarque :

On peut faire un parallèle avec un raisonnement par l’absurde : si on suppose qu’une propriété est vraie et, qu’en déroulant un raisonnement, on trouve une contradiction, on pourra en conclure que la supposition de départ était fausse. En revanche, si on ne trouve aucune contradiction, cela ne prouve en aucun cas que la proposition de départ est vraie…

 

 Un intervalle de confiance étant un intervalle de confiance numérique, il est incorrect de conclure la détermination d’un intervalle de confiance par une phrase du type : p  a une probabilité de 0.95 d' être dans
  car il n’y a plus d’aléatoire à ce stade. Il est en revanche convenable d’écrire :

« L’intervalle est un intervalle de confiance

de la proportion inconnue p  au niveau de confiance 0,95 . »

 

      Exemples d’exercices en classe de terminale

 

Enoncés

Propositions de corrigés

 

Commentaire :

Pour toute question, vous pouvez consulter le document ressource ou nous contacter à l’adresse :  referentmath02@ac-bordeaux.fr