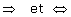« La démonstration est constitutive de l’activité mathématique et les élèves doivent en prendre conscience. Faire en sorte que les élèves puissent concevoir des démonstrations dans leur globalité, puis en détailler les différentes étapes a toujours été et reste un objectif essentiel de tout enseignement des mathématiques en France ».

(Programme et document d’accompagnement de première S)

Classe de seconde

Source : document d’accompagnement du programme de mathématiques de la classe de seconde (Orientations générales / § 6. Rédaction, logique, notations - pages 4 et 5 de la brochure)

[…]

En classe de seconde, les problèmes de logique mathématique concernent essentiellement l'implication et l'équivalence, la manipulation du contre-exemple, le "ou" et le "et". Il ne s'agit pas bien sûr de faire des cours de logique formelle, mais on n'hésitera pas à aborder les problèmes de logique lorsqu'ils se présentent, notamment lors du travail écrit. On n'oubliera pas qu'au collège, seule l'implication est utilisée : toute équivalence logique y est formulée en deux énoncés séparés en termes de "si … alors …" ; en seconde, on abordera le "si et seulement si". On pourra utiliser les symboles 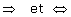, mais avec prudence et modération.

Les symboles 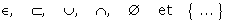seront employés à bon escient et sans excès. Les quantificateurs  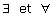ne sont pas au programme de la seconde ; on soulignera cependant l'universalité de la plupart des énoncés mathématiques ; à propos d'une propriété portant sur un ensemble E, on insistera sur le fait que la seule exhibition d'un contre exemple suffit à démontrer qu'elle est fausse et que si E est un ensemble infini, aucune liste finie de cas où elle est vraie n'en constitue une démonstration. La notation 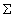 sera introduite à l'occasion de travaux sur la moyenne en statistique, sans pour autant l'utiliser systématiquement.

Classe de première de la série scientifique

Source : document d’accompagnement des programmes de mathématiques -  la classe de première des séries générales (À propos de la démonstration- page 50 de la brochure)

[…]

Une place particulière est réservée en mathématiques au langage symbolique : on en évitera tout excès ; mieux vaut privilégier le langage français usuel. L’abus d’expressions symboliques amène certains élèves à confondre symboles mathématiques et système d’abréviations, voire - cas extrême - à croire que c’est faire des mathématiques que d’habiller un texte de symboles ou de termes spécifiques.

[…]

Source : document d’accompagnement des programmes de mathématiques la classe terminale de la série scientifique (Enseigner les mathématiques - construire un corpus / Démontrer -  page 27 de la brochure)

[…]

La déduction usuelle (par implication ou équivalence) et la manipulation du contre-exemple ont été travaillées en seconde ; des problèmes bien choisis permettront d’aborder en première le raisonnement par contraposition, par l’absurde ou par disjonction des cas ; […]

Classe terminale de la série scientifique

Source : document d’accompagnement des programmes de mathématiques la classe terminale de la série scientifique(Enseigner les mathématiques - construire un corpus / Démontrer)

page 27 de la brochure

[…]

le raisonnement par récurrence relève de la classe terminale.

pages 28 et 29  de la brochure

[…]

Certains élèves peuvent avoir besoin de clarifier divers niveaux de langage ou d’écriture utilisés en mathématiques. On peut, pour ceux-là, s’inspirer de la classification faite en français, où l’on distingue les niveaux suivants : soutenu (vocabulaire et syntaxe recherchés, précis), courant (vocabulaire usuel et correct), familier (langue peu surveillée qui présente des écarts avec le vocabulaire et la syntaxe corrects) et relâché (langue très libre et souvent incorrecte) (voir Méthodes et pratiques du français au lycée, Magnard, 2000). En mathématiques, le langage pourra être familier voire relâché au brouillon ou lors de certaines prises de notes ; il sera soutenu lors de l’écriture des théorèmes et des phases essentielles de résolution ; il pourra être courant dans tous les autres cas.

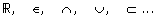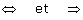L’utilisation de symboles mathématiques ( ) est indispensable mais doit rester modérée. Une place à part est néanmoins à faire aux connecteurs logiques ( ) : leur utilisation ne doit pas prendre la place de liens de langage tels que d’où, donc, on en déduit que, il s’ensuit que… ; toute rédaction doit comporter une part de phrases en langue française. Quant aux quantificateurs « pour tout…» et « il existe…», présents en permanence dans la plupart des propositions mathématiques, ils pourront être abrégés (en particulier au brouillon) à l’aide des symboles 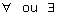 que l’on pourra introduire au fur et à mesure de l’année.

[…]

Quelques situations d’utilisation des différents raisonnements

Un article du bulletin Réciproques n°15