Restitution organisée de connaissances |
Équipe académique Mathématiques,
|
Les textes officiels
Objectifs de l’épreuve du Baccalauréat
L'épreuve est destinée à évaluer la façon dont les candidats ont atteint les grands objectifs de formation mathématique visés par le programme de la série ES ou de la série S :
Acquérir des connaissances et les organiser
| Série ES
|
Série S
|
Recommandations destinées aux concepteurs de sujets
| Série ES … La restitution organisée de connaissances (comme l'exposé d'une question citée en exemple dans le programme),… l'application directe de résultats ou de méthodes,… la formulation d'un raisonnement sont des trames possibles. |
Série S … La restitution organisée de connaissances (comme par exemple la rédaction d’une démonstration figurant au programme), l'application directe de résultats ou de méthodes,… la formulation d’un raisonnement sont des trames possibles. |
Les objectifs
Inciter l’élève à apprendre le cours ;
Inciter l’élève à mieux réfléchir
aux démarches mises en œuvre ;
Valoriser le travail personnel de l’élève sérieux
;
Évaluer de manière directe la maîtrise des compétences
de base ;
Introduire la pratique de l’étude de démonstration chez
les élèves des séries scientifiques.
La démonstration est constitutive de l’activité mathématique et les élèves doivent en prendre conscience
Remarque
De nombreux élèves de série S se destinent à des études scientifiques. Ils doivent avoir rencontré en classe et pratiqué suffisamment de démonstrations pour ne pas être désarçonnés en entrant dans le supérieur.
La place dans le sujet
Soit lors d’un exercice spécifique (à 3 points) plutôt en
ES
Soit répertoriée « restitution organisée
de connaissance » dans un exercice. plutôt en S
Les compétences mises en jeu
Maîtriser la lecture d’un graphique, d’un tableau, d’une courbe
Traiter une information (par exemple passer d’un cadre graphique à un
cadre algébrique)
Appliquer directement le cours
Énoncer un (plusieurs) théorème(s) ou une (plusieurs) définition(s)
Argumenter, justifier
Savoir imaginer un exemple ou un contre-exemple
Maîtriser la logique
Comprendre en profondeur une notion
Faire preuve d’esprit critique
La question de ROC demande à l’élève une part de réflexion et d’argumentation et le place plus en mode de compréhension que d’exécution.
La forme
La « restitution organisée de connaissances » offre la possibilité d’évaluer des connaissances de type exécution, mais également d’évaluer la compréhension des notions utilisées par les élèves.
Il peut s’agir :
- de l’application directe du cours (éventuellement sous forme de QCM)
- de citer une définition ou un théorème utilisé
Exemples
Série ES (banque décembre 2004)
Exercice n° 4 : utilisation du sens de variations de fonctions de référence sur un intervalle pour trouver le sens de variation de la fonction composée.
Exercice n° 5 : Lecture d’une courbe, lien entre aire sous une courbe et intégrale, rappel de la définition d’une valeur moyenne.
– d’expliquer en quoi un résultat est faux, en quoi un résultat est juste ;
Série ES (banque décembre 2004)
Exercice n° 6 : Repérer une valeur numérique « aberrante » pour une probabilité, la modifier pour que deux évènements soient indépendants.
Exercice n° 7 : Lecture d’un tableau de variations, questions sous forme de Vrai-Faux, il faut justifier lorsque l’on dit « Vrai »
Série S (banque décembre 2004 - enseignement obligatoire)
Exercice n° 5 : Distinguer les notions « f est continue en a » et « f est dérivable en a » en produisant un exemple si la situation proposée est valide ou en justifiant à l’aide d’un théorème dans le cas contraire.
Exercice n° 6 : Suite majorée, suite croissante, suite tendant vers plus l’infini ; traduction mathématique et travail de logique entre ces notions.
– de démontrer un résultat du cours
À ce sujet on notera que la démonstration de cours n’est pas la seule modalité de la restitution organisée de connaissances et que chaque démonstration de cours demandée est contextualisée. Cela signifie que la démonstration est demandée dans un cas particulier ou sur un exemple – les prérequis sont alors bien précisés dans le texte et la consigne doit être claire (« ne pas utiliser le théorème dans le cas général »…) – ou que la démonstration est demandée au sein d’un exercice dans lequel le résultat est utilisé – ceci pour éviter le bachotage ou l’utilisation d’une banque de données sur calculatrice.
Exemples
Série S uniquement (banque décembre 2004)
Exercice n° 1 : formules sur les combinaisons
Exercice n° 7 : argument d’un quotient de deux nombres complexes
Exercice n° 9 (spécialité) : « il existe une unique similitude directe ….. »
Exercice n° 11 : fonction exponentielle
Exercice n° 13 : une suite croissante non majorée
Exercice n° 15 : exemple de fonction continue
et croissante sur R+, dérivabilité de 
etc.
Quelques critères susceptibles de
mesurer la difficulté de la question posée
Le nombre d’informations pertinentes à collecter et à
traiter ;
Le nombre de traitements (transformations internes à un
registre) et le degré de difficulté de ceux-ci ;
L’existence de changements de registres et le degré de
difficulté de ceux-ci ;
Le nombre de théorèmes à citer.
Pour information
Voici la liste des démonstrations qui apparaissent dans le libellé du programme avec la mention « on démontrera », ou « on montrera », ou « on établira ».
En enseignement obligatoire
1. Une suite croissante non majorée tend vers l’infini.
2. Théorème des “gendarmes” pour les fonctions lorsque la variable tend vers l’infini.
3. Corollaire du théorème des valeurs intermédiaires : « Si f est une fonction continue strictement monotone sur [a ; b], alors pour tout réel k compris entre f (a) et f (b), l’équation f(x) = k a une solution unique dans [a ; b] ».
4. Unicité de la fonction dérivable sur R telle que f’ = f et f (0)=1.
5. Détermination de la limite en
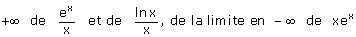
6. Si f est continue sur un intervalle I, et si a est un point
de I, la fonction F telle que 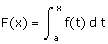est l’unique primitive de f sur I s’annulant
en a. (démonstration dans le cas où f est continue et croissante).
7. Existence et unicité de la solution de y’ = ay + b passant par un point donné.
8. La fonction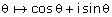 
vérifie l’équation fonctionnelle caractéristique
des fonctions exponentielles.
9. Formules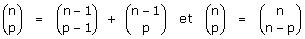 
En enseignement de spécialité
1. L’ensemble des nombres premiers est infini.
2. Une similitude ayant deux points fixes est l’identité ou une symétrie axiale.
3. Étant donnés quatre points A, B, A’ et B’ tels que A ≠ B et A’ ≠ B’, il existe une similitude directe unique transformant A en A’ et B en B’.
Remarque
Cette liste reprend uniquement les démonstrations explicitement mentionnées dans le programme ; il ne faut pas considérer que ce sont les seules démonstrations à présenter aux élèves ; chaque professeur adapte son enseignement au niveau de sa classe.
Ce n’est pas non plus une liste des démonstrations « à apprendre par cœur » et qui reviendraient telles quelles dans les sujets de Bac.
Il faut familiariser les élèves à des types de démonstrations, pour leur permettre d’en repérer les principes, et de pouvoir les réinvestir dans le cadre d’un exercice, sous une forme contextualisée.
Cette pratique doit être progressive et commencer dès la première S, voire dès la classe de seconde.
On se reportera aux nombreux exemples fournis dans la banque d’exercices de décembre 2004, comme indiqué plus haut.
Consulter la synthèse de l'atelier