Bordeaux, mars 2002
| 1. Graphes : notions de base |
| Eric Sopena, Professeur au département Informatique
de l'IUT Bordeaux 1 Bordeaux, mars 2002 |
| 1.1 Modélisation |
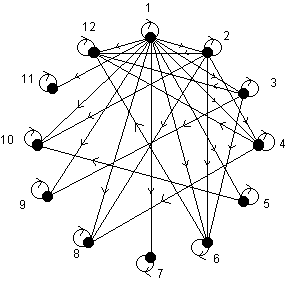
Construire un graphe orienté dont les sommets sont les entiers compris entre 1 et 12 et dont les arcs représentent la relation « être diviseur de ».
Une chèvre, un chou et un loup se trouvent sur la rive d’un fleuve ; un passeur souhaite les transporter sur l’autre rive mais, sa barque étant trop petite, il ne peut transporter qu’un seul d’entre eux à la fois. Comment doit-il procéder afin de ne jamais laisser ensemble et sans surveillance le loup et la chèvre, ainsi que la chèvre et le chou ?
Trois maris jaloux et leurs épouses souhaitent traverser une rivière.
Ils disposent d’une barque qui ne peut transporter plus de deux personnes à
la fois. Comment doivent-ils procéder, sachant qu’aucune femme ne doit rester
en compagnie d’un ou deux hommes sans que son mari soit présent ?
Montrez que ce problème n’a pas de solution si les couples sont au nombre de
4.
On souhaite prélever 4 litres de liquide dans un tonneau. Pour cela, nous avons à notre disposition deux récipients (non gradués !), l’un de 5 litres, l’autre de 3 litres... Comment doit-on faire ?
Deux joueurs disposent de 2 ou plusieurs tas d’allumettes. A tour de rôle, chaque joueur peut enlever un certain nombre d’allumettes de l’un des tas (selon la règle choisie). Le joueur qui retire la dernière allumette perd la partie.
¨Modéliser ce jeu à l’aide d’un graphe
dans le cas où l’on dispose au départ de deux tas contenant chacun trois allumettes,
et où un joueur peut enlever une ou deux allumettes à chaque fois.
¨Que doit jouer le premier joueur pour
gagner la partie à coup sûr ?
¨Mêmes questions avec 3 tas de 3 allumettes.
Essayez d’exprimer (et non nécessairement de résoudre…) en termes de graphes les problèmes suivants :
¨Peut-on placer huit dames
sur un échiquier sans qu’aucune d’elles ne puisse en prendre une autre ?
¨Un cavalier peut-il se déplacer sur
un échiquier en passant sur chacune des cases une fois et une seule ?
¨Combien doit-on placer de dames sur
un échiquier 5x5 afin de contrôler toutes les cases ?
|
Le graphe ci-contre représente le plan des couloirs d’un musée. Un gardien placé dans un couloir peut surveiller les deux carrefours placés à ses extrémités. Combien de gardiens sont nécessaires (et comment les placer) afin que tous les carrefours soient surveillés ? Si l’on place maintenant les gardiens aux carrefours, en supposant qu’un tel gardien peur surveiller tous les couloirs amenant à ce carrefour, combien de gardiens sont nécessaires ? |
|
Sept élèves, désignés par A,B,C,D,E,F et G se sont rendus à la bibliothèque aujourd’hui. Le tableau suivant précise « qui à rencontré qui » (la bibliothèque étant petite, deux élèves présents au même moment se rencontrent nécessairement…).
¨Quel est l’ordre d’arrivée
des élèves à la bibliothèque ?
¨leur ordre de départ ?
|
élève |
A |
B |
C |
D |
E |
F |
G |
|
a rencontré |
D,E |
D,E,F,G |
E,G |
A,B,E |
A,B,C,D,F,G |
B,E,G |
B,C,E,F |
|
Dans le graphe biparti ci-contre, les sommets T1, …, T6
représentent des travailleurs et les sommets E1, …, E6 des emplois. |
|
Chaque jour, un groupe de 12 enfants fait une promenade, par rang de deux. Combien de jours peuvent-ils se promener si l’on souhaite qu’un enfant n’ait jamais deux fois le même voisin ? Et si maintenant la promenade se fait par rang de trois ?
Soit X un ensemble de lapins, et G un graphe orienté ayant X pour ensemble de sommets. On dit que G est un « graphe de parenté » si les arcs de G codent la relation « être l’enfant de »… Quelles conditions doit nécessairement vérifier G pour pouvoir être un graphe de parenté ?
| Fin des exercices sur les notions de base (modélisation) |
Construire un graphe orienté dont les sommets sont les entiers compris entre 1 et 12 et dont les arcs représentent la relation « être diviseur de ».
Aucune difficulté particulière (ne pas oublier les boucles)…
Une chèvre, un chou et un loup se trouvent sur la rive d’un fleuve ; un passeur souhaite les transporter sur l’autre rive mais, sa barque étant trop petite, il ne peut transporter qu’un seul d’entre eux à la fois. Comment doit-il procéder afin de ne jamais laisser ensemble et sans surveillance le loup et la chèvre, ainsi que la chèvre et le chou ?
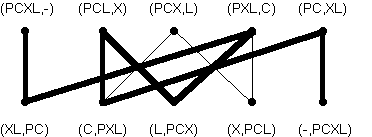
Cette situation peut être modélisée à l’aide d’un graphe. Désignons par P le passeur, par C la chèvre, par X le chou et par L le loup. Les sommets du graphe sont des couples précisant qui est sur la rive initiale, qui est sur l’autre rive. Ainsi, le couple (PCX,L) signifie que le passeur est sur la rive initiale avec la chèvre et le chou (qui sont donc sous surveillance), alors que le loup est sur l’autre rive. Une arête relie deux sommets lorsque le passeur peut passer (sic) d’une situation à l’autre. En transportant la chèvre, le passeur passe par exemple du sommet (PCX,L) au sommet (X,PCL). Le graphe ainsi obtenu est biparti : les sommets pour lesquels le passeur est sur la rive initiale ne sont reliés qu’aux sommets pour lesquels le passeur est sur l’autre rive…
Naturellement, on ne considèrera pas les sommets dont l’une des composantes est CX ou LC car ces situations sont interdites.
Il suffit ensuite de trouver un chemin (le plus court par exemple) entre la situation initiale (PCXL,-) et la situation finale souhaitée (-,PCXL). La figure suivante donne un tel chemin :
Trois maris jaloux et leurs épouses souhaitent traverser une rivière.
Ils disposent d’une barque qui ne peut transporter plus de deux personnes
à la fois. Comment doivent-ils procéder, sachant qu’aucune femme ne doit rester
en compagnie d’un ou deux hommes sans que son mari soit présent ?
Montrez que ce problème n’a pas de solution si les couples sont au nombre
de 4.
La solution est donnée dans les vers suivants :
« It duplex mulier, nedit una, vehit que manentem ;
Itque una, utuntur tunc duo puppe viri.
Par vadit, redeunt bini ; mulierque so rorem
Ad vehit ; ad propriam sive maritus abit. »
Pour les non latinistes, il est possible d’utiliser le même principe que dans l’exercice précédent, en notant A, B et C les femmes, a, b et c les maris. On obtient encore un graphe biparti, selon que la barque est sur une rive ou sur l’autre. Le schéma suivant propose une solution parmi d’autres (le graphe n’est pas représenté en totalité)…
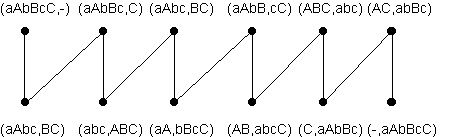
Dans le cas où quatre couples sont sur la berge, les sommets (aAbBcCdD,-) et (-,aAbBcCdD) sont dans des composantes connexes distinctes. Il n’existe donc pas de chemin de l’un à l’autre et le problème n’a pas de solution (on peut vérifier que dans la composante connexe du sommet d’arrivée, seuls figurent des sommets correspondant à un seul mari sur la rive initiale)…
À titre d’exercice supplémentaire, on peut voir que le problème des 4 maris jaloux a une solution s’il existe une île au milieu de la rivière permettant de déposer certaines personnes ou si la barque peut transporter trois personnes.
On souhaite prélever 4 litres de liquide dans un tonneau. Pour cela, nous avons à notre disposition deux récipients (non gradués !), l’un de 5 litres, l’autre de 3 litres... Comment doit-on faire ?
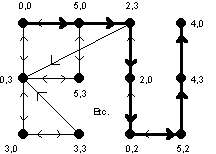
Toujours le même principe. Les sommets sont cette fois des couples donnant le contenu du récipient de 5 litres et celui du récipient de 3 litres. On place un arc entre deux sommets lorsqu’on peut passer d’une configuration à l’autre. On cherche alors un chemin du sommet 0,0 au sommet 4,0… La figure suivante montre un tel chemin (le graphe n’est pas représenté en entier…)
Deux joueurs disposent de 2 ou plusieurs tas d’allumettes. A tour de rôle, chaque joueur peut enlever un certain nombre d’allumettes de l’un des tas (selon la règle choisie). Le joueur qui retire la dernière allumette perd la partie.
¨Modéliser ce jeu à l’aide d’un graphe
dans le cas où l’on dispose au départ de deux tas contenant chacun trois allumettes,
et où un joueur peut enlever une ou deux allumettes à chaque fois.
¨Que doit jouer le premier joueur
pour gagner la partie à coup sûr ?
¨Mêmes questions avec 3 tas de 3 allumettes.
Le jeu avec 2 tas de trois allumettes est décrit par le graphe suivant (tous les arcs sont orientés de gauche à droite) :
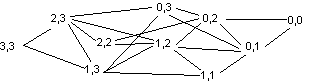
Le joueur qui atteint la configuration 0,0 perd la partie. Pour gagner, on doit donc atteindre la configuration 0,1 ou 0,2. On peut vérifier qu’en jouant 1,3 au premier coup, quelle que soit la réponse de l’adversaire, on peut atteindre ensuite 0,1 ou 0,2. Le coup gagnant au départ est donc « enlever 2 allumettes dans un tas ».
Pour trois tas de trois allumettes, c’est simplement un peu plus long ;-)…
Essayez d’exprimer (et non nécessairement de résoudre…) en termes de graphes les problèmes suivants :
¨Peut-on placer huit dames
sur un échiquier sans qu’aucune d’elles ne puisse en prendre une autre ?
¨Un cavalier peut-il se déplacer sur
un échiquier en passant sur chacune des cases une fois et une seule ?
¨Combien doit-on placer de dames sur
un échiquier 5x5 afin de contrôler toutes les cases ?
Pour chacune de ces questions, on construit un graphe dont les sommets représentent les cases de l’échiquier. Les arêtes sont alors définies ainsi :
1 et 3 : une arête relie deux cases si une dame placée sur l’une contrôle l’autre,
2 : une arête relie deux cases si un cavalier placée sur l’une peut se rendre sur l’autre.
Les 3 problèmes s’expriment alors ainsi en terme de graphes :
1 : Trouver un ensemble maximal de sommets tels qu’il n’existe aucune arête entre ces sommets (un tel ensemble est dit indépendant).
2 : Trouver un chemin hamiltonien (c’est-à-dire un chemin passant une et une seule fois par chacun des sommets).
3 : Trouver un ensemble minimal de sommets tel que tout sommet appartient à cet ensemble ou est relié par une arête à au moins l’un des sommets de cet ensemble (un tel ensemble est dit dominant).

La figure ci-dessus donne une solution pour chacun de ces trois problèmes. Le parcours du cavalier présenté est en fait un cycle hamiltonien (le cavalier retourne à son point de départ).
|
Le graphe ci-contre représente le plan des couloirs d’un musée. Un gardien placé dans un couloir peut surveiller les deux carrefours placés à ses extrémités. Combien de gardiens sont nécessaires (et comment les placer) afin que tous les carrefours soient surveillés ? Si l’on place maintenant les gardiens aux carrefours, en supposant qu’un tel gardien peur surveiller tous les couloirs amenant à ce carrefour, combien de gardiens sont nécessaires ? |
|
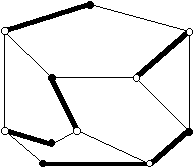
1. Chaque gardien va être placé sur une arête et pourra surveiller deux carrefours (sommets). Le graphe ayant 11 sommets, il faudra au minimum 6 gardiens. Il faut donc trouver un ensemble (minimal) d’au moins six arêtes, tel que tout sommet est incident à au moins l’une de ces arêtes. Le schéma ci-dessous donne une solution (arêtes épaisses).
2. Cette fois, les gardiens sont sur les sommets et surveillent les arêtes. Il faut trouver un ensemble minimal de sommets tel que toute arête est incidente à au moins l’un de ces sommets. On constate rapidement que tout cycle de longueur 5 doit avoir 3 sommets dans cet ensemble… Le schéma ci-dessous donne une solution utilisant 6 sommets (sommets blancs).
Sept élèves, désignés par A,B,C,D,E,F et G se sont rendus à la bibliothèque aujourd’hui. Le tableau suivant précise « qui à rencontré qui » (la bibliothèque étant petite, deux élèves présents au même moment se rencontrent nécessairement…).
¨Quel est l’ordre d’arrivée
des élèves à la bibliothèque ?
¨leur ordre de départ ?
|
élève |
A |
B |
C |
D |
E |
F |
G |
|
a rencontré |
D,E |
D,E,F,G |
E,G |
A,B,E |
A,B,C,D,F,G |
B,E,G |
B,C,E,F |
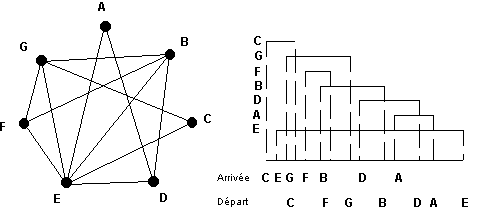
Le premier travail consiste à dessiner le « graphe des rencontres ». Ce graphe est ce que l’on appelle un graphe d’intervalles : chaque sommet est associé à un intervalle (le temps de présence de l’élève dans la bibliothèque) et deux sommets sont reliés lorsque les intervalles s’intersectent (les élèves se sont croisés). Pour notre exemple, plusieurs solutions sont alors possibles, chacune pouvant donner des ordres d’arrivée et de départ différents. Le schéma suivant en fournit une…
|
Dans le graphe biparti ci-contre, les sommets T1, …,
T6 représentent des travailleurs et les sommets E1, …, E6 des emplois.
|
|
Affecter un emploi à une personne revient à « sélectionner » une arête. Chaque personne ne pouvant occuper qu’un seul emploi, et un emploi ne pouvant être occupé que par une seule personne, il faut donc sélectionner un nombre maximal d’arêtes de façon telle que ces arêtes n’ont aucun sommet commun (un tel ensemble est qualifié de stable maximal). Le schéma ci-dessous donne un tel ensemble (arêtes épaisses) composé de 6 arêtes…
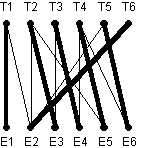
Chaque jour, un groupe de 12 enfants fait une promenade, par rang de deux. Combien de jours peuvent-ils se promener si l’on souhaite qu’un enfant n’ait jamais deux fois le même voisin ? Et si maintenant la promenade se fait par rang de trois ?
Considérons le graphe complet K12 à 12 sommets, chaque sommet représentant un enfant. Le nombre d’arêtes de ce graphe est 12 x 11 / 2 = 66. Une promenade correspond à un ensemble de 6 arêtes non incidentes : chaque arête représente un rang (deux enfants) et chaque enfant ne peut appartenir qu’à un seul rang lors d’une promenade. Ainsi, le nombre maximum de promenades est 11. Une solution possible pour ces 11 promenades est la suivante (les enfants, ou sommets, sont désignés par 1,2,…,12) :
1-2, 3-12, 4-11, 5-10, 6-9, 7-8 2-3, 12-4, 11-5, 10-6, 9-7, 8-1
1-3, 4-2, 5-12, 6-11, 7-10, 8-9 3-4, 2-5, 12-6, 11-7, 10-8, 9-1
1-4, 5-3, 6-2, 7-12, 8-11, 9-10 4-5, 3-6, 2-7, 12-8, 11-9, 10-1
1-5, 6-4, 7-3, 8-2, 9-12, 10-11 5-6, 4-7, 3-8, 2-9, 12-10, 11-1
1-6, 7-5, 8-4, 9-3, 10-2, 11-12 6-7, 5-8, 4-9, 3-10, 2-11, 12-1
1-7, 2-12, 3-11, 4-10, 5-9, 6-8
Les cinq premières « paires » de promenades sont obtenues en découpant de deux façons complémentaires un cycle à 12 sommets (pour la première ligne, il s’agit du cycle 1,2,3,12,4,11,5,10,6,9,7,8,1). La dernière ligne est composée des 6 arêtes restantes.
Considérons maintenant le cas des rangs de trois. Chaque rang correspond alors à un triangle dans K12 et chaque promenade à un ensemble de 4 triangles « disjoints ». Cette fois, une promenade utilise 4 x 3 = 12 arêtes et le nombre maximum de promenades est 5…
Je n’ai pas de solution « sous la main »…. Je publierai donc la première solution qui me parviendra… ;-)
Soit X un ensemble de lapins, et G un graphe orienté ayant X pour ensemble de sommets. On dit que G est un « graphe de parenté » si les arcs de G codent la relation « être l’enfant de »… Quelles conditions doit nécessairement vérifier G pour pouvoir être un graphe de parenté ?
Voici une liste de conditions nécessaires :
Ÿ Chaque sommet doit avoir un degré entrant égal à 2 (chaque lapin a deux parents) à l’exception de deux sommets pour lesquels le degré entrant est nul (ces sommets correspondent aux « Adam » et « Ève » de notre groupe de lapins…).
Ÿ Le graphe doit être sans circuit (on dit également acyclique). En effet, un lapin ne peut avoir pour parent l’un de ses descendants…
Ÿ On doit pouvoir colorier les sommets de ce graphe en deux couleurs (male et femelle), de façon telle que tout sommet de degré entrant égale à 2 possède un prédécesseur male et un prédécesseur femelle.
Ÿ Il est possible que d’autres conditions soient nécessaires mais ma connaissance du mécanisme de reproduction chez les lapins ne me permet pas d’aller plus loin… (nombre de portées possibles, nombre de petits lapins par portée, etc.)