Graphes, notions de base : degré des sommets

¨Construisez de tels graphes ayant 4 sommets, 5 , 6 , 7 .
¨Qu’en déduisez-vous ?
¨Prouvez-le !

La situation est-elle identique pour les graphes dont tous les sommets sont de degré 4 ?

Une suite décroissante (au sens large) d’entiers est graphique s’il existe un graphe dont les degrés des sommets correspondent à cette suite (par exemple, le triangle à trois sommets correspond à la suite 2,2,2). Les suites suivantes sont-elles graphiques ?

¨Trouvez deux graphes distincts (c’est-à-dire non isomorphes [1] ) correspondant à la suite 3, 2, 2, 2, 1.

Pour les graphes orientés, il faut considérer des suites de couples d’entiers (le premier élément d’un couple correspond au degré entrant, le second au degré sortant). Les suites suivantes sont-elles des suites graphiques ?

Essayez de construire un graphe non orienté ayant au moins deux sommets et tel que tous les sommets ont des degrés distincts. Qu’en déduisez-vous ?

Montrez que dans un groupe de six personnes, il y en a nécessairement trois qui se connaissent mutuellement ou trois qui ne se connaissent pas (on suppose que si A connaît B, B connaît également A).
Montrez que cela n’est plus nécessairement vrai dans un groupe de cinq personnes.

Montrez que dans un groupe de 9 personnes, 4 se connaissent mutuellement ou 3 ne se connaissent pas.
Cela est-il toujours vrai dans un groupe de 8 personnes ?

Montrez que dans un groupe de personnes, il y a toujours deux personnes ayant le même nombre d’amis présents.

Un groupe de personnes est tel que :
(i) chaque personne est membre d’exactement deux associations,
(ii) chaque association comprend exactement trois membres,
(iii) deux associations quelconques ont toujours exactement un membre en commun.
Combien y a-t-il de personnes ? d’associations ?

[1] deux graphes G1 et G2 sont isomorphes s’il existe une bijection f entre leurs ensembles de sommets qui préserve les arêtes (f(x)f(y) est une arête de G2 si et seulement si xy est une arête de G1).

¨Construisez de tels graphes ayant 4 sommets, 5 , 6 , 7 .
¨Qu’en déduisez-vous ?
¨Prouvez-le !

Les graphes dont tous les sommets sont de degré trois sont appelés graphes 3-reguliers ou graphes cubiques. La figure ci-dessous montre deux graphes cubiques, ayant respectivement 4 et 6 sommets. En effet, on constate aisément qu’il n’existe pas de graphes cubiques ayant un nombre impair de sommets : le nombre d’arêtes d’un graphe cubique à n sommets est 3n/2 qui n’est entier que lorsque n est pair.

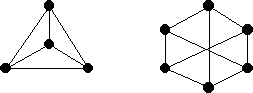
La situation est-elle identique pour les graphes dont tous les sommets sont de degré 4 ?

Cette fois, le nombre d’arêtes d’un tel graphe est 4n/2 = 2n si n est le nombre de sommets. De tels graphes existent toujours… dès que n est au moins égal à 5 !

Considérons par exemple le graphe dont les sommets sont les entiers de 0 à n-1 (avec n ³ 5) et les arêtes les paires de sommets i,j telles que j = i+1 ou j = i+2 (modulo n). On vérifie aisément que ces graphes sont 4-réguliers (tout sommet i est relié à i-2, i-1, i+1 et i+2, toujours modulo n…).

¨Trouvez deux graphes distincts (c’est-à-dire non isomorphes [1] ) correspondant à la suite 3, 2, 2, 2, 1.

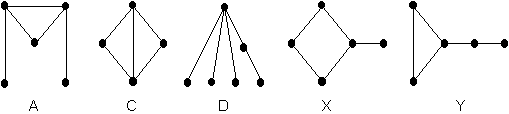
Les suites (3,3,2,1,1), (3,3,2,2) et (4,2,1,1,1,1) sont graphiques, comme le montrent les graphes A, C et D de la figure ci-dessous. Les graphes X et Y sont distincts et correspondent tous deux à la suite (3,2,2,2,1).

Nous savons que la somme des degrés entrants doit être égale à la somme des degrés sortants. Nous pouvons ainsi déjà éliminer les suites

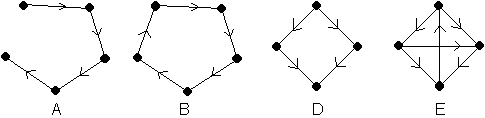
Les suites [0,1),(1,1),(1,1),(1,1),(1,0)], [(1,1),(1,1),(1,1),(1,1),(1,1)], [(0,2),(1,1),(1,1),(2,0)] et [(1,2),(1,2),(2,1),(2,1)] sont graphiques, comme le montrent respectivement les graphes A, B, D et E ci-dessous.

Essayez de construire un graphe non orienté ayant au moins deux sommets et tel que tous les sommets ont des degrés distincts. Qu’en déduisez-vous ?

On s’aperçoit rapidement que c’est impossible. Ainsi, dans un graphe, il existe toujours deux sommets de même degré. La preuve de ce fait est donnée dans la solution de l’exercice 19.

Supposons tout d’abord qu’il existe une personne, disons A, en connaissant trois autres, disons B, C et D, et considérons les relations entre B, C et D… Si deux d’entre elles se connaissent (par exemple B et C) alors elles forment avec A un trio de personnes se connaissant mutuellement. Dans le cas contraire, B, C et D forment un trio ne se connaissant pas.

Si aucune personne n’en connaît trois autres, on raisonne de façon symétrique en considérant la personne A et trois personnes qu’elle ne connaît pas : si ces trois personnes se connaissent mutuellement, c’est gagné. Sinon, deux personnes parmi ces trois ne se connaissant pas forment avec A un trio de personnes ne se connaissant pas…

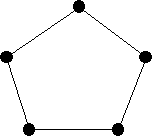
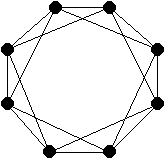
Le graphe suivant montre que la situation est différente pour un groupe de cinq personnes (tout triplet de personnes contient 1 ou 2 arêtes)…

Montrez que dans un groupe de 9 personnes, 4 se connaissent mutuellement ou 3 ne se connaissent pas.
Cela est-il toujours vrai dans un groupe de 8 personnes ?

Un tel groupe sera représenté sous forme d’un graphe dont les sommets sont les personnes ; une arête reliera deux sommets correspondant à des personnes se connaissant. Supposons qu’il existe un groupe (graphe) de 9 personnes (sommets) n’ayant pas la propriété annoncée. Nous allons montrer que nous aboutissons nécessairement à une contradiction.

Prenons tout d’abord deux personnes se connaissant, disons A et B (si personne ne se connaît, nous avons un trio ne se connaissant pas). Les sept autres personnes peuvent alors être réparties en quatres groupes : G, le groupe des personnes ne connaissant ni A ni B ; GA, le groupe des personnes connaissant A mais ne connaissant pas B ; GB, le groupe des personnes connaissant B mais ne connaissant pas A ; GAB, le groupe des personnes connaissant A et B.

Ÿ G : ce groupe est nécessairement composé de personnes se connaissant mutuellement (sinon, deux personnes de ce groupe ne se connaissant pas formeraient avec A ou B un trio ne se connaissant pas). Ainsi, ce groupe contient au maximum 3 personnes (sinon nous avons un quatuor se connaissant mutuellement).

Ÿ GA : ce groupe est nécessairement composé de personnes se connaissant mutuellement (sinon, deux personnes de ce groupe ne se connaissant pas formeraient avec B un trio ne se connaissant pas). Ainsi, ce groupe contient au maximum 2 personnes (sinon nous avons avec A un quatuor se connaissant mutuellement).

Ÿ GB : de façon symétrique, ce groupe est nécessairement composé de personnes se connaissant mutuellement (sinon, deux personnes de ce groupe ne se connaissant pas formeraient avec A un trio ne se connaissant pas). Ainsi, ce groupe contient au maximum 2 personnes (sinon nous avons avec B un quatuor se connaissant mutuellement).

Ÿ GAB : ce groupe est nécessairement composé de personnes ne se connaissant pas (sinon, deux personnes de ce groupe se connaissant formeraient avec A et B un quatuor se connaissant mutuellement). Ce groupe contient donc au maximum deux personnes (sinon nous avons un trio ne se connaissant pas).

Ÿ toutes les personnes de GB connaissent toutes les personnes de G (sinon une personne de GB et une personne de G ne se connaissant pas formeraient avec A un trio ne se connaissant pas). L’union de G et GB est donc un ensemble de personnes se connaissant mutuellement et sa taille est d’au plus 3 (sinon nous avons un quatuor se connaissant mutuellement).

Ÿ de façon symétrique, les personnes de G et GA se connaissent mutuellement et la taille de l’union de G et GA est d’au plus 3.

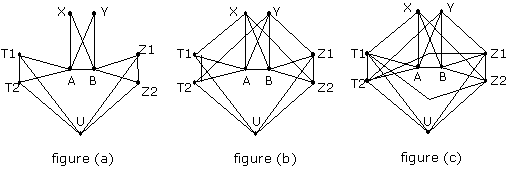
Fort de ces observations, on peut vérifier sans peine que la seule possibilité concernant les cardinalités de ces 3 groupes est la suivante : card(G) = 1, card(GA) = 2, card(GB) = 2 et card(GAB) = 2 (avec A et B, nous retrouvons bien nos 9 personnes…). Posons alors G = {U}, GA = {T1, T2}, GB = {Z1, Z2} et GAB = {X, Y}. Le schéma correspondant est donné ci-dessous, figure (a).

Considérons maintenant les relations entre GAB et GA, GB… Tout sommet de GA ou GB doit être relié à au moins un sommet de GAB (sinon nous avons un trio ne se connaissant pas). Par contre, les deux sommets de GA (ou de GB) ne peuvent être reliés au même sommet de GAB, sinon, ils formeraient avec A (ou B) un quatuor se connaissant mutuellement. Nous obtenons ainsi la figure (b) ci-dessous (du fait des symétries, une seule solution est possible).

Qu’en est-il des relations entre GA et GB ? Z1 est nécessairement voisin de T2, sinon Z1, T2 et X forment un trio ne se connaissant pas. De la même façon, Z2 est nécessairement voisin de T1 (voir figure (c)).

Pour conclure sur une contradiction, il nous reste à regarder les relations entre G et GAB… U est nécessairement relié à X ou Y, sinon U,X,Y serait un trio ne se connaissant pas. Si U est relié à X, alors X,U,T1 et Z2 forment un quatuor se connaissant mutuellement et si U est relié à Y, alors U,Y,T2 et Z1 forment un quatuor se connaissant mutuellement. Dans les deux cas, nous obtenons la contradiction recherchée…

Le graphe suivant montre que la propriété n’est plus vérifiée pour un groupe de 8 personnes :

Montrez que dans un groupe de personnes, il y a toujours deux personnes ayant le même nombre d’amis présents.

Construisons un graphe dont les sommets représentent les personnes et plaçons une arête entre deux sommets lorsque les personnes correspondantes sont amies. Dire que deux personnes ont le même nombre d’amis revient à dire que deux sommets dans le graphe ont même degré…

Nous allons montrer qu’il n’existe aucun graphe dont tous les sommets ont des degrés distincts. Supposons qu’un tel graphe existe et qu’il possède n sommets. Le degré maximal d’un sommet est donc n-1. Si tous les degrés des sommets sont distincts, on a donc nécessairement un sommet de degré 0, un sommet de degré 1, …, un sommet de degré n-1. Du fait de la présence d’un sommet de degré 0, disons x₀, il est impossible d’avoir un sommet de degré n-1 ! (en effet, celui-ci devrait être relié à tous les autres, y compris x₀). On obtient ainsi une contradiction.

Supposons que nous avons n associations et considérons le graphe complet K_n dont les sommets représentent les associations (toute paire d’associations est donc reliée par une arête). Deux associations ayant toujours exactement un membre en commun, nous pouvons étiqueter l’arête reliant ces deux associations par le membre en question. Par ailleurs, chaque personne étant membre d’exactement deux associations, une même personne ne peut pas étiqueter deux arêtes distinctes (sinon elle appartiendrait à au moins trois associations). Les arêtes sont donc en bijection avec les personnes…

Finalement, chaque association comprenant exactement trois personnes, tous les sommets du graphe complet sont de degré 3. Il s’agit donc de K₄ ! Le nombre d’associations est donc de 4 (nombre de sommets) et le nombre de personnes de 6 (nombre d’arêtes = 4 x 3 / 2).

3, 3, 2, 1, 1	3, 3, 2, 2	5, 3, 2, 1, 1, 1
3, 3, 1, 1	4, 2, 1, 1, 1, 1	5, 4, 3, 1, 1, 1, 1

3, 3, 2, 1, 1	3, 3, 2, 2	5, 3, 2, 1, 1, 1
3, 3, 1, 1	4, 2, 1, 1, 1, 1	5, 4, 3, 1, 1, 1, 1