Bordeaux, mars 2002
| 1. Graphes : notions de base |
| Eric Sopena, Professeur au département Informatique
de l'IUT Bordeaux 1 Bordeaux, mars 2002 |
| 1.3 Graphes eulériens |
Est-il possible de tracer les figures suivantes sans lever le crayon (et sans passer deux fois sur le même trait !…) ? Pourquoi ?
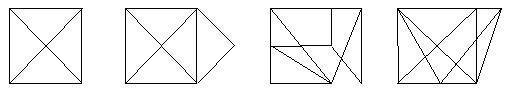
Est-il possible de tracer une courbe, sans lever le crayon, qui coupe chacun des 16 segments de la figure suivante ?

Est-il possible de traverser les sept ponts de la ville de Koenigsberg en empruntant deux fois chaque pont, dans un sens puis dans l’autre ?
Soit G un graphe non Eulérien. Est-il toujours possible de rendre G Eulérien en lui rajoutant un sommet et quelques arêtes ?
On considère des dominos dont les faces sont numérotées 1, 2, 3, 4 ou 5.
¨En excluant les dominos doubles,
de combien de dominos dispose-t-on ?
¨Montrez que l’on peut arranger ces
dominos de façon à former une boucle fermée (en utilisant la règle habituelle
de contact entre les dominos).
¨Pourquoi n’est-il pas nécessaire de
considérer les dominos doubles ?
¨Si l’on prend maintenant des dominos
dont les faces sont numérotées de 1 à n, est-il possible de les arranger
de façon à former une boucle fermée ?
| Fin des exercices sur les notions de base (graphes eulériens) |
Est-il possible de tracer les figures suivantes sans lever le crayon (et sans passer deux fois sur le même trait !…) ? Pourquoi ?
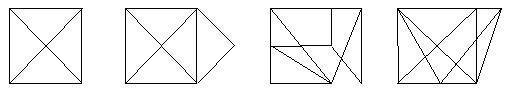
De tels tracés sont possibles si le graphe correspondant admet un chemin eulérien, c’est-à-dire s’il contient exactement 0 ou 2 sommets de degré impair. La réponse est donc positive uniquement pour la deuxième figure…
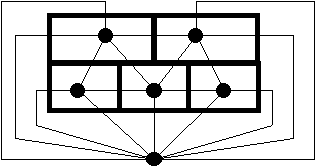
Est-il possible de tracer une courbe, sans lever le crayon, qui coupe chacun des 16 segments de la figure suivante ?

On peut associer un graphe à cette figure (en réalité un multigraphe car nous aurons des arêtes multiples) de la façon suivante : les sommets représentent les régions (y compris la région extérieure) et deux sommets sont reliés par autant d’arêtes que le nombre de segments communs de leurs régions (voir ci-dessous).
Le problème revient alors à effectuer un chemin eulérien dans ce graphe. Or, ce graphe contient 4 sommets de degré impair… c’est donc impossible.
Est-il possible de traverser les sept ponts de la ville de Koenigsberg en empruntant deux fois chaque pont, dans un sens puis dans l’autre ?
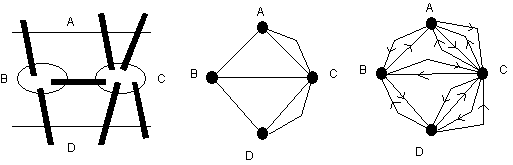
La figure suivante représente les ponts de Koenigsberg et le graphe non orienté associé au problème classique. Le problème consistant à emprunter deux fois chaque pont, dans un sens puis dans l’autre, revient à chercher un cycle eulérien dans le graphe orienté obtenu en modélisant chaque pont par deux arcs de directions opposées. On peut observer que le graphe orienté ainsi obtenu est tel que tout sommet possède un degré entrant égal à son degré sortant (cela est vrai pour tout graphe orienté obtenu à partir d’un graphe non orienté en remplaçant chaque arête par deux arcs de directions opposées…). Le graphe orienté est donc eulérien et le parcours suivant le prouve (les ponts, ou arcs, sont désignés par AB, BC, BD, AC1, AC2, CD1, CD2 dans un sens puis BA, DB, CD1, etc. dans l’autre sens) :
AB, BD, DC1, CA1, AC1, CD1, DB, BA, AC2, CB, BC, CD2, DC2, CA2
Soit G un graphe non Eulérien. Est-il toujours possible de rendre G Eulérien en lui rajoutant un sommet et quelques arêtes ?
Pour qu’un graphe soit eulérien, il faut et il suffit que tous ses sommets soient de degré pair. Si un graphe contient k sommets impairs, il est possible de rajouter un nouveau sommet x, relié à ces k sommets. Dans le graphe obtenu, les k sommets considérés sont devenus pairs… Cependant, le degré de x étant k, le graphe n’est toujours pas eulérien si k était impair…
Remarquons qu’il est possible de rajouter des arêtes entre les sommets de degré impair dans le graphe d’origine… Mais l’ajout d’une telle arête, entre deux sommets impairs a et b par exemple, fait que le nombre de sommets impairs devient k-2, qui a la même parité que k…
La réponse est donc : ce n’est possible que si le nombre de sommets impairs est pair…
On considère des dominos dont les faces sont numérotées 1, 2, 3, 4 ou 5.
¨En excluant les dominos
doubles, de combien de dominos dispose-t-on ?
¨Montrez que l’on peut arranger ces
dominos de façon à former une boucle fermée (en utilisant la règle habituelle
de contact entre les dominos).
¨Pourquoi n’est-il pas nécessaire
de considérer les dominos doubles ?
¨Si l’on prend maintenant des dominos
dont les faces sont numérotées de 1 à n, est-il possible de les arranger
de façon à former une boucle fermée ?
Les dominos sont au nombre de 4 + 3 + 2 + 1 = (4 x 5) / 2 = 10 :
1-2, 1-3, 1-4, 1-5, 2-3, 2-4, 2-5, 3-4, 3-5, 4-5
Considérons maintenant le graphe complet K5 à 5 sommets. Ce graphe possède 10 arêtes, chaque arête correspondant à une paire de sommets distincts… c’est-à-dire à un domino. Former une boucle fermée avec ces dominos revient donc à trouver un cycle eulérien (passant par toutes les arêtes, donc utilisant tous les dominos) dans K5. Une solution possible est la suivante : 1-2, 2-3, 3-4, 4-5, 5-1, 1-3, 3-5, 5-2, 2-4, 4-1.
Les dominos doubles peuvent être insérés sans difficulté dans cette suite. En terme de graphes, les dominos doubles correspondent à une boucle sur un sommet et cette boucle peut être « parcourue » lorsqu’on atteint le sommet en question pour la première fois par exemple…
Si l’on considère le même problème avec des faces numérotées de 1 à n, on doit raisonner sur le graphe complet à n sommets. Or, nous savons qu’un graphe admet un cycle eulérien si et seulement si il est connexe et ne possède que des sommets de degré pair. Dans le cas des graphes complets, cela n’est vrai que si le nombre de sommets est impair…