Bordeaux, mars 2002
| 2. Graphes : problèmes de coloration |
| Eric Sopena, Professeur au département Informatique
de l'IUT Bordeaux 1 Bordeaux, mars 2002 |
Tout graphe contenant un triangle (K3) ne peut être colorié en moins de trois couleurs.
¨Construire un graphe sans
triangle qui nécessite également trois couleurs.
¨Comment, à partir du graphe précédent,
construire un graphe sans K4 nécessitant 4 couleurs ?
¨un graphe sans K5 nécessitant
5 couleurs ?
Déterminer le nombre chromatique des graphes suivants :

|
Le schéma ci-contre représente un carrefour. Le tableau suivant précise les « franchissements » possibles de ce carrefour.
|
|
|
¨Modélisez ces
incompatibilités à l’aide d’un graphe dont les sommets représentent les
franchissements possibles et les arêtes les incompatibilités entre franchissements. |
|
On cherche à colorier le graphe ci-contre en utilisant des entiers positifs de façon telle que deux sommets voisins ont des couleurs dont la différence, en valeur absolue, est au moins égale à trois.
|
|
|
¨Maintenant, on souhaite que, de plus, deux sommets à distance deux aient des couleurs dont la différence, en valeur absolue, est au moins égale à deux. Quelle est la meilleure coloration possible de ce graphe ? |
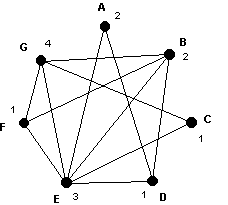
Sept élèves, désignés par A,B,C,D,E,F et G se sont rendus à la bibliothèque aujourd’hui. Le tableau suivant précise « qui à rencontré qui » (la bibliothèque étant petite, deux élèves présents au même moment se rencontrent nécessairement…).
|
élève |
A |
B |
C |
D |
E |
F |
G |
|
a rencontré |
D,E |
D,E,F,G |
E,G |
A,B,E |
A,B,C,D,F,G |
B,E,G |
B,C,E,F |
De combien de places assises doit disposer la bibliothèque pour que chacun ait pu travailler correctement au cours de cette journée ?
| Fin des exercices sur les problèmes de coloration |
Tout graphe contenant un triangle (K3) ne peut être colorié en moins de trois couleurs.
¨Construire un graphe sans
triangle qui nécessite également trois couleurs.
¨Comment, à partir du graphe précédent,
construire un graphe sans K4 nécessitant 4 couleurs ?
¨un graphe sans K5 nécessitant
5 couleurs ?
Il suffit de considérer par exemple un cycle ayant un nombre impair de sommets. Si l’on rajoute à ce graphe un sommet relié à tous les sommets du cycle, on obtient un graphe de nombre chromatique 4 ne contenant pas de K4. On peut itérer cette construction de façon à obtenir, pour tout k, un graphe de nombre chromatique k ne contenant pas de Kk. Un résultat plus puissant, dû à Erdös, montre que pour tout k, il existe un graphe de nombre chromatique k sans triangle, et même sans cycle de longueur inférieure à un entier p donné, quel que soit p…
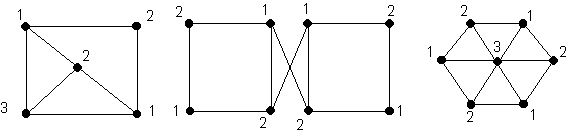
Déterminer le nombre chromatique des graphes suivants :

Les graphes suivants ont respectivement pour nombre chromatique 3, 2 et 3 :
|
Le schéma ci-contre représente un carrefour. Le tableau suivant précise les « franchissements » possibles de ce carrefour.
|
|
|
¨Modélisez ces
incompatibilités à l’aide d’un graphe dont les sommets représentent les
franchissements possibles et les arêtes les incompatibilités entre franchissements. |
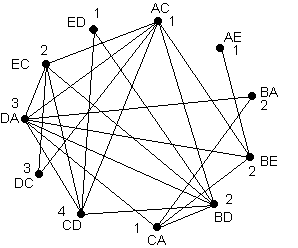
Le graphe modélisant le carrefour est représenté ci-dessous. Son nombre chromatique est égal à 4 (il est 4-coloriable et contient un K4 regroupant les sommets AC, BD, CD et DA). Un ensemble de sommets de même couleur, par exemple ED, AC, AE et CA regroupe un ensemble de trajets pouvant s’effectuer en même temps (aucune incompatibilité). Le nombre chromatique correspond alors au nombre minimum de « cycles » que doivent respecter les feux de signalisation de ce carrefour. Pour notre exemple, nous aurons :
1. ED, AC, AE et CA 2. BA, BE, BD et EC 3. DC et DA 4. CD
D’autres solutions (4-colorations) sont naturellement possibles…
|
On cherche à colorier le graphe ci-contre en utilisant des entiers positifs de façon telle que deux sommets voisins ont des couleurs dont la différence, en valeur absolue, est au moins égale à trois.
|
|
|
¨Maintenant, on souhaite que, de plus, deux sommets à distance deux aient des couleurs dont la différence, en valeur absolue, est au moins égale à deux. Quelle est la meilleure coloration possible de ce graphe ? |
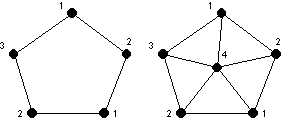
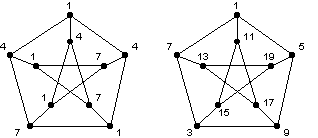
Voici deux colorations du graphe de Petersen. La première utilise 7 comme plus grand entier, la deuxième 19…
Dans le premier cas, on peut vérifier que pour colorier ainsi un cycle à 5 sommets, la meilleure solution est 1-4-1-4-7. Ainsi, il n’est pas possible de n’utiliser que des entiers inférieurs à 7.
Dans le deuxième cas, remarquons que deux sommets quelconques sont à distance au plus 2 (on dit que le graphe est de diamètre 2). Toutes les couleurs doivent donc être distinctes et « espacées » de 2. La meilleure solution utilise ainsi les entiers impairs 1,3,5,…,19.
Sept élèves, désignés par A,B,C,D,E,F et G se sont rendus à la bibliothèque aujourd’hui. Le tableau suivant précise « qui à rencontré qui » (la bibliothèque étant petite, deux élèves présents au même moment se rencontrent nécessairement…).
|
élève |
A |
B |
C |
D |
E |
F |
G |
|
a rencontré |
D,E |
D,E,F,G |
E,G |
A,B,E |
A,B,C,D,F,G |
B,E,G |
B,C,E,F |
De combien de places assises doit disposer la bibliothèque pour que chacun ait pu travailler correctement au cours de cette journée ?
On reprend le « graphe des rencontres » proposé dans l’exercice 8. Il reste alors à proposer une coloration du graphe utilisant un nombre minimum de couleurs. Chaque couleur correspondra à une place assise. La coloration suivante montre que 4 places sont nécessaires… et suffisantes car le graphe contient une clique (sous-graphe complet) à 4 sommets (B-E-F-G).