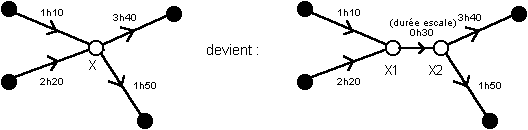3. Graphes : problèmes de chemins

Eric Sopena, Professeur au département Informatique de l'IUT Bordeaux 1 Bordeaux, mars 2002 Parcourir le cahier

Exercice 31

Un tournoi est un graphe orienté tel que toute paire de sommets est reliée par un arc, dans un sens ou dans l’autre (mais pas dans les deux sens).
¨Pourquoi, selon vous, appelle-t-on de tels graphes des tournois ?
¨Montrez que si un tournoi contient un circuit de longueur k, alors il contient également des circuits de longueur k’, pour tout k’ < k (une « preuve » à l’aide d’un dessin suffit…).
¨Dessinez un tournoi à 6 sommets ne possédant pas de circuit de longueur 4.

Exercice 32

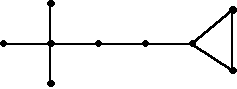
Un robot se promène sur le graphe ci-contre. Partant d’un sommet quelconque s, appelé sommet de stockage, il doit déposer un cube sur chacun des autres sommets. Il possède suffisamment de cubes sur le sommet de stockage, mais ne peut transporter qu’un cube à la fois (il doit donc repasser par le sommet de stockage avant de livrer un autre cube). Calculer, pour chacun des sommets du graphe, le trajet minimum que doit parcourir le robot si ce sommet est sommet de stockage.

Quel est le « meilleur » sommet de stockage ?

Exercice 34

Construire le graphe orienté dont les sommets sont les entiers compris entre 1 et 24 et dont les arcs relient x à y lorsque x divise y. De plus, les arcs sont valués par le quotient y/x (ainsi, l’arc allant de 3 vers 15 a la valeur 5).
¨Comment reconnaît-on dans ce graphe un nombre premier ?
¨Comment retrouver dans ce graphe la décomposition d’un nombre en facteurs premiers ?

Exercice 35

Remplir le tableau ci-dessous qui, pour le graphe valué ci-contre, donne la valeur du plus court chemin d’un sommet à un autre.

Exercice 36

Exécutez l’algorithme de Dijkstra sur le graphe précédent, à partir du sommet C, puis à partir du sommet F.

Fin des exercices sur les problèmes de chemins

Parcourir le cahier

Exercice 31

Un tournoi est un graphe orienté tel que toute paire de sommets est reliée par un arc, dans un sens ou dans l’autre (mais pas dans les deux sens).
¨Pourquoi, selon vous, appelle-t-on de tels graphes des tournois ?
¨Montrez que si un tournoi contient un circuit de longueur k, alors il contient également des circuits de longueur k’, pour tout k’ < k (une « preuve » à l’aide d’un dessin suffit…).
¨Dessinez un tournoi à 6 sommets ne possédant pas de circuit de longueur 4.

Dans un « tournoi », un ensemble de n individus (ou équipes) se rencontrent deux à deux, chaque rencontre se soldant par la victoire de l’un et la défaite de l’autre… Ceci peut être représenté à l’aide d’un graphe dont les sommets correspondent aux individus et tel qu’un arc va du sommet A vers le sommet B si la rencontre correspondante a vu la victoire de A sur B…

Supposons qu’un tournoi T possède un circuit C = x₁x₂…x_kx₁ de longueur k > 3 (en effet, pour k=3, il n’y a rien à prouver). Nous allons d’abord montrer que T possède un circuit de longueur 3.

Considérons n’importe quel sommet du circuit C, x₁ par exemple. Nous affirmons qu’il existe nécessairement un arc x_ix_i+1 dans T, avec 1 < i < k, tel que x₁x_i et x_j+1x₁ sont des arcs (en d’autres termes, x₁x_ix_i+1x₁ forme un circuit). On peut exhiber un tel arc en « tournant » autour de C de la façon suivante :

Ÿ   posons i=2 ; si x₃x₁ est un arc, nous avons gagné (x₁x₂x₃x₁ est un circuit) ; dans le cas contraire, x₁x₃ est un arc et nous pouvons poser i=3…

Ÿ   en continuant de la sorte, nous allons nécessairement trouver un arc x_ix_i+1 ayant la propriété cherchée car x_kx₁ est un arc de T (au pire, la solution sera donc l’arc x_k-1x_k).

Nous allons terminer la preuve en montrant que dès que nous avons un circuit de taille k’ composé de sommets de C, avec 3 £ k’ < k-1, nous avons nécessairement un circuit de taille k’+1, toujours composé de sommets de C (nous montrons ainsi une propriété plus forte que celle annoncée dans l’exercice).

Soit donc C’ = y₁y₂…y_k’y₁ un circuit composé de sommets de C et notons X l’ensemble des sommets de C non utilisés dans C’.

Supposons qu’il existe un sommet x de X qui soit successeur de certains sommets de C’ et prédécesseur d’autres sommets de C’. Dans ce cas, il y a nécessairement un arc y_jy_j+1 dans C’ tel que y_j est prédécesseur de x et y_j+1 est successeur de x. Nous avons alors un circuit de longueur k’+1 : y₁y₂…y_jxy_j+1…x_k’x₁ (nous avons pris ici un « raccourci » dans l’écriture car l’arc y_jy_j+1 peut être l’arc y_ky₁…).

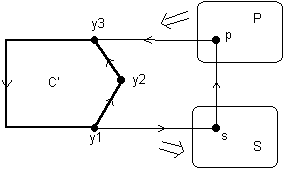
Si on ne peut trouver un tel sommet x, cela signifie que l’ensemble X peut être partitionné en deux sous-ensembles S et P respectivement composés des sommets successeurs de tous les sommets de C’ et des sommets prédécesseurs de tous les sommets de C’. Aucun de ces deux sous-ensembles ne peut être vide car nous savons qu’un circuit unit les sommets x₁,…,x_k. Pour la même raison, il existe nécessairement un sommet s dans S et un sommet p dans P tel que sp est un arc dans T. (Dans le cas contraire, l’ensemble S (ou P) n’aurait que des prédécesseurs (ou des successeurs) parmi les autres sommets et le circuit initial C ne pourrait exister).

Nous avons alors un circuit de longueur k’+1, donné par y₁spy₃…y_k’y₁ (voir figure ci-dessous).

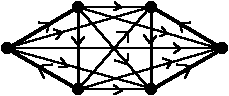
Finalement, la figure suivante montre un tournoi à 6 sommets ne possédant aucun circuit de longueur supérieure à 3 (ce tournoi est composé de 2 circuits de longueur 3 réunis par des arcs ayant tous la même direction) :

Exercice 32

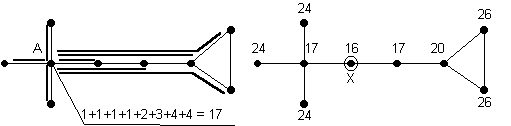
Un robot se promène sur le graphe ci-contre. Partant d’un sommet quelconque s, appelé sommet de stockage, il doit déposer un cube sur chacun des autres sommets. Il possède suffisamment de cubes sur le sommet de stockage, mais ne peut transporter qu’un cube à la fois (il doit donc repasser par le sommet de stockage avant de livrer un autre cube). Calculer, pour chacun des sommets du graphe, le trajet minimum que doit parcourir le robot si ce sommet est sommet de stockage.

Quel est le « meilleur » sommet de stockage ?

Pour un sommet donné, il est nécessaire de calculer la somme des longueurs des plus courts chemins de ce sommet aux autres sommets. La figure suivante donne cette valeur pour le sommet A, puis pour tous les sommets du graphe. Le meilleur sommet de stockage est donc le sommet X…

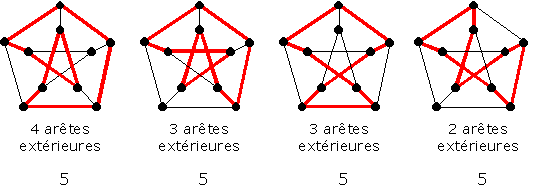
On peut essayer d’énumérer les cycles de longueur 5 par rapport au nombre d’arêtes « extérieures » qu’ils contiennent. La figure suivante montre les « schémas » de cycles correspondants et le nombre de tels cycles obtenus par rotation… Le nombre total de cycles de longueur 5 est donc 12…

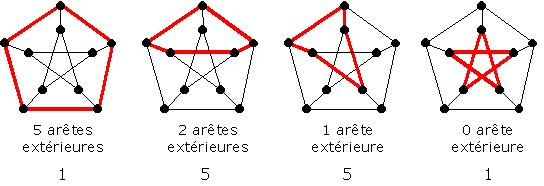
Même principe pour les cycles de longueur 6, au nombre de 10 :

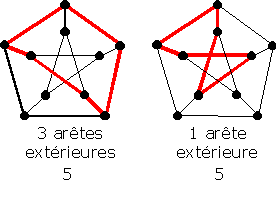
Les cycles de longueur 8, au nombre de 15 :

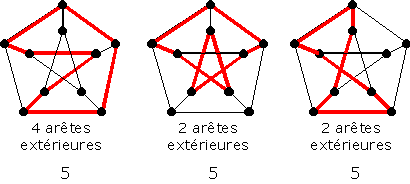
Et enfin les cycles de longueur 9, au nombre de 20 :

Exercice 34

Construire le graphe orienté dont les sommets sont les entiers compris entre 1 et 24 et dont les arcs relient x à y lorsque x divise y. De plus, les arcs sont valués par le quotient y/x (ainsi, l’arc allant de 3 vers 15 a la valeur 5).
¨Comment reconnaît-on dans ce graphe un nombre premier ?
¨Comment retrouver dans ce graphe la décomposition d’un nombre en facteurs premiers ?

Un nombre premier correspond à un sommet de degré entrant 2 puisqu’il doit être divisible par 1 et lui-même (n’oublions pas la boucle présente en chaque sommet), ou de degré entrant 1 (car 1 est premier et n’est divisible que par lui même).

Si l’on considère un chemin allant de 1 à n, le produit des valeurs des arcs qui le composent vaut nécessairement n… On peut alors, dans le graphe précédent, ne conserver que les arcs dont la valeur est un nombre premier et qui ne sont pas des boucles. Tout sommet n est alors tel qu’il existe un unique chemin de 1 à n, dont les valeurs d’arcs donnent la décomposition en facteurs premiers.

Exercice 35

Remplir le tableau ci-dessous qui, pour le graphe valué ci-contre, donne la valeur du plus court chemin d’un sommet à un autre.

Le calcul peut se faire directement… On obtient le tableau suivant :

Exercice 36

Exécutez l’algorithme de Dijkstra sur le graphe précédent, à partir du sommet C, puis à partir du sommet F.

Exercice 36

À partir du sommet C, nous obtenons :

fin de l’algorithme….

À partir du sommet F, nous obtenons :

fin de l’algorithme….

Il suffit de dessiner le graphe dont les sommets sont les villes et les arcs les dessertes de la compagnie, en valuant chaque arc par la durée du vol correspondant. Un algorithme de plus court chemin permet alors de résoudre le problème.

Pour prendre en compte les durées d’escale, deux méthodes sont possibles :

1. Modifier l’algorithme précédent, en incluant dans le calcul du coût d’un chemin les durées d’escale…

2. Transformer le graphe selon le principe décrit ci-dessous. L’algorithme reste alors le même, en choisissant « correctement » les sommets de départ et d’arrivée (sans escale) : on part donc de Départ2 et on arrive en Arrivée1…