Bordeaux, mars 2002
| 5. Graphes : problèmes d’automates |
| Eric Sopena, Professeur au département Informatique
de l'IUT Bordeaux 1 Bordeaux, mars 2002 |
5.1 Automates simples
Proposez un automate déterministe permettant de reconnaître un entier positif inférieur ou égal à 138.
Proposez des automates déterministes permettant de reconnaître :
|
¨les
multiples de 3, |
¨les multiples
de 100, |
¨les multiples
de 50, |
Proposez un automate déterministe permettant de reconnaître un horaire donné sous la forme 12:15.
Proposez un automate déterministe permettant de reconnaître une date donnée sous la forme 03/02 (pour le 3 février), en se limitant à l’année en cours…
5.2 Automates avec actions
Un élève peut être considéré comme un système très particulier : lorsqu’il est interrogé oralement par un enseignant, il répond s’il est en forme et ne répond pas s’il est fatigué. Après avoir été interrogé, un élève en forme devient fatigué. Lorsqu’une interrogation surprise se présente, l’élève en forme remet une bonne copie, l’élève fatigué une copie plutôt moyenne. Après une interrogation surprise, tous les élèves sont fatigués pour le reste de la journée ! Le soir, tous les élèves se reposent et arrivent en forme le lendemain matin.
Modélisez cette situation à l’aide d’un automate avec actions (on pourra dans un premier temps établir la liste des événements « subis » par un élève et la liste des actions réalisées par celui-ci en réponse à ces événements…)
Un téléphone portable est finalement un objet assez simple… Quand vous le sortez de son emballage, il est éteint et toutes les touches sont sans effet… sauf la touche « ON », qui émet un « bip » sympathique et voici votre téléphone allumé… Dorénavant, toutes les touches émettent un « bip » (c’est amusant ;-)… même la touche « OFF » qui, pourtant, éteint votre téléphone…
¨Modélisez le fonctionnement de ce téléphone portable à l’aide d’un automate avec actions.
On n’arrête pas le progrès… Votre téléphone est également muni d’une touche « MUTE » qui, naturellement, n’a aucun effet si votre téléphone est éteint, mais qui peut faire passer votre téléphone (allumé en mode normal) en mode silencieux (après avoir émis cependant un « bip » ;-). En mode silencieux, les touches n’émettent plus de « bip », sauf la touche « MUTE » qui, du coup, fait repasser votre téléphone en mode normal… Là où l’on prend vraiment conscience du progrès accompli, c’est que lorsque vous rallumez un téléphone qui a été éteint en mode normal, il se rallume en mode normal, alors que s’il a été éteint en mode silencieux, il se rallume en mode silencieux (en émettant cependant un « bip »…). Étonnant, non ?
¨ Proposez un nouvel automate avec actions pour ce téléphone « moderne »...
Le Kidor-Dyn est un animal fabuleux que peu d’entre nous ont eu le loisir de croiser sur leur chemin... À sa naissance (vers 7h00 du matin), le Kidor-Dyn a faim et soif. Lorsqu’il passe près d’une rivière, il boit, et cela lui suffit pour la journée. Lorsqu’il croise une belette, il la croque, et cela lui suffit pour la journée. Il peut cependant, au hasard des rencontres, croquer une seconde belette mais jamais trois dans la même journée. Lorsque le soleil se couche, le Kidor-Dyn fait sa toilette et s’endort, qu’il ait croisé ou pas de rivière ou de belette dans la journée... Le lendemain, il a à nouveau faim et soif, à moins qu’il n’ait rêvé, au cours de la nuit, de pluie (auquel cas il n’a pas soif) ou de belette (auquel cas il n’a pas faim). Par ailleurs, chaque fois qu’un enfant passe à proximité de lui dans la journée, le Kidor-Dyn chante une chanson...
¨Modéliser la vie trépidante du Kidor-Dyn à l’aide d’un automate avec actions.
| Fin des exercices sur les automates |
5.1 Automates simples
Proposez un automate déterministe permettant de reconnaître un entier positif inférieur ou égal à 138.
L’automate suivant reconnaît les entiers souhaités en écriture normalisée. Toutes les transitions non représentées vont vers un états puits.
Proposez des automates déterministes permettant de reconnaître :
|
¨les
multiples de 3, |
¨les multiples
de 100, |
¨les multiples
de 50, |
Voici les automates correspondants. Toutes les transitions non représentées vont vers un états puits.
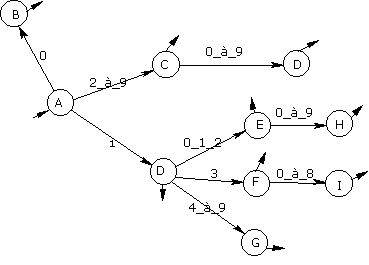
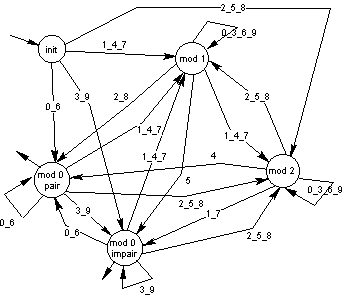
¨ les multiples de 3 : aucune difficulté particulière, on raisonne « modulo 3 »…
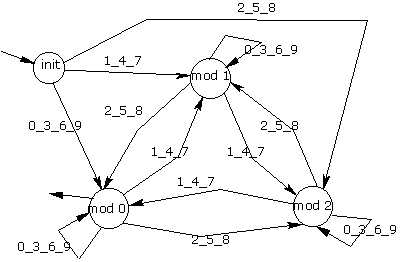
¨ les multiples de 9 : il suffit de généraliser l’exemple précédent… Un état « init » et 9 états, « mod 0 » à « mod 8 ». On obtient ainsi un « graphe complet » à 9 sommets (non dessiné ici… ;-).
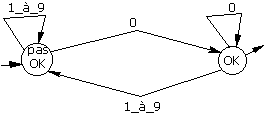
¨ les multiples de 10 : il faut reconnaître les entiers terminés par 0… La difficulté réside dans le fait que l’automate doit rester déterministe. Ainsi, lorsqu’on lit un 0, on va dans l’état d’acceptation, quitte à en revenir dès qu’un chiffre différent de 0 apparaît…
¨ les multiples de 100 : même principe, avec deux zéros pour finir…
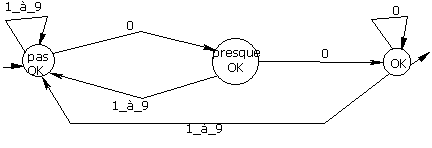
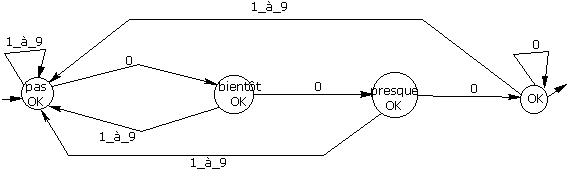
¨ les multiples de 1000 : one more time… and one more zero…
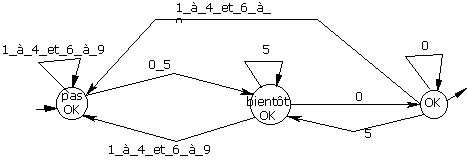
¨ les multiples de 50 : cette fois, les entiers doivent être terminés par 00 ou 50.
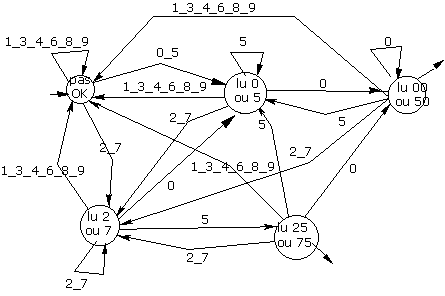
¨ les multiples de 25 : cette fois, les entiers doivent être terminés par 00, 25, 50 ou 75. Il faut bien penser à la « signification » des états de l’automate…
¨ les multiples de 250 : cette fois, les entiers doivent être terminés par 000, 250, 500 ou 750. Même principe que pour le précédent…
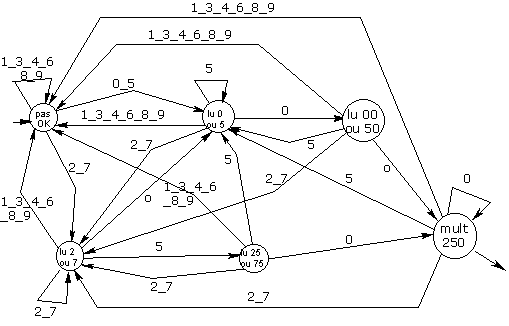
¨ les multiples de 6 : ils sont multiples de trois… et pairs ! On peut ainsi partir de l’automate reconnaissant les multiples de trois et le « modifier » afin de séparer les pairs et les impairs sur l’état final (en séparant également les transitions arrivant et sortant de cet état)…
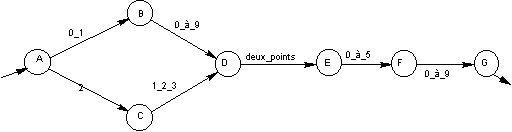
Proposez un automate déterministe permettant de reconnaître un horaire donné sous la forme 12:15.
L’automate suivant reconnaît les heures sous une forme « normalisée » (03:07 pour trois heures et 7 minutes). Le premier symbole doit être 0, 1 ou 2. Si c’est 2, alors seuls 1, 2 ou 3 sont autorisés ensuite. Les minutes sont sur deux chiffres et doivent commencer par 0, 1, 2, 3, 4 ou 5…
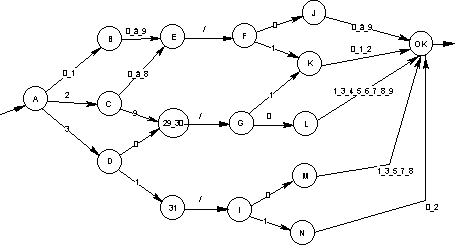
Proposez un automate déterministe permettant de reconnaître une date donnée sous la forme 03/02 (pour le 3 février), en se limitant à l’année en cours…
Le mois de février 2002 comportant 28 jours, nous obtenons l’automate ci-dessous. Il est nécessaire de distinguer les jours 29 ou 30 (interdits en février) et les jours 31. Ces jours aboutissent respectivement dans les états « 29_30 » et « 31 ». Il suffit alors de ne retenir par la suite que les mois où ces jours sont autorisés…
5.2 Automates avec actions
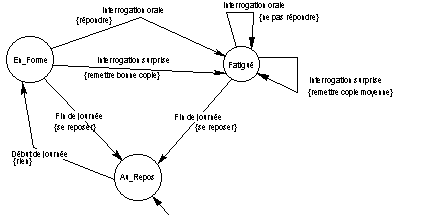
Un élève peut être considéré comme un système très particulier : lorsqu’il est interrogé oralement par un enseignant, il répond s’il est en forme et ne répond pas s’il est fatigué. Après avoir été interrogé, un élève en forme devient fatigué. Lorsqu’une interrogation surprise se présente, l’élève en forme remet une bonne copie, l’élève fatigué une copie plutôt moyenne. Après une interrogation surprise, tous les élèves sont fatigués pour le reste de la journée ! Le soir, tous les élèves se reposent et arrivent en forme le lendemain matin.
Modélisez cette situation à l’aide d’un automate avec actions (on pourra dans un premier temps établir la liste des événements « subis » par un élève et la liste des actions réalisées par celui-ci en réponse à ces événements…)
Les éléments de cet automate seront les suivants :
¨ événements : interrogation orale, interrogation surprise, fin de journée, début de journée.
¨ actions : répondre, ne pas répondre, remettre une bonne copie, remettre une copie moyenne, se reposer
¨ états : en forme, fatigué, au repos
L’automate peut alors être représenté ainsi (on suppose qu’à sa « naissance », l’élève est au repos…). Les actions sont données entre accolades.
Un téléphone portable est finalement un objet assez simple… Quand vous le sortez de son emballage, il est éteint et toutes les touches sont sans effet… sauf la touche « ON », qui émet un « bip » sympathique et voici votre téléphone allumé… Dorénavant, toutes les touches émettent un « bip » (c’est amusant ;-)… même la touche « OFF » qui, pourtant, éteint votre téléphone…
¨Modélisez le fonctionnement de ce téléphone portable à l’aide d’un automate avec actions.
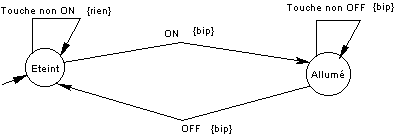
Aucune difficulté particulière. Deux états, « éteint » et « allumé » permettent de distinguer les réactions du téléphone aux événements que sont les touches…
L’automate correspondant est le suivant :
On n’arrête pas le progrès… Votre téléphone est également muni d’une touche « MUTE » qui, naturellement, n’a aucun effet si votre téléphone est éteint, mais qui peut faire passer votre téléphone (allumé en mode normal) en mode silencieux (après avoir émis cependant un « bip » ;-). En mode silencieux, les touches n’émettent plus de « bip », sauf la touche « MUTE » qui, du coup, fait repasser votre téléphone en mode normal… Là où l’on prend vraiment conscience du progrès accompli, c’est que lorsque vous rallumez un téléphone qui a été éteint en mode normal, il se rallume en mode normal, alors que s’il a été éteint en mode silencieux, il se rallume en mode silencieux (en émettant cependant un « bip »…). Étonnant, non ?
¨ Proposez un nouvel automate avec actions pour ce téléphone « moderne »...
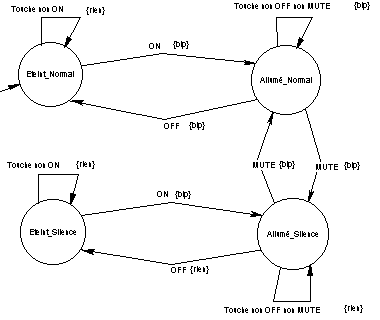
Cette fois, il est nécessaire de distinguer les états de fonctionnement selon le mode « normal » ou « silencieux »… De la même façon, on distinguera les états d’arrêt, selon que le téléphone a été arrêté en mode « normal » ou « silencieux »…
L’automate est alors le suivant :
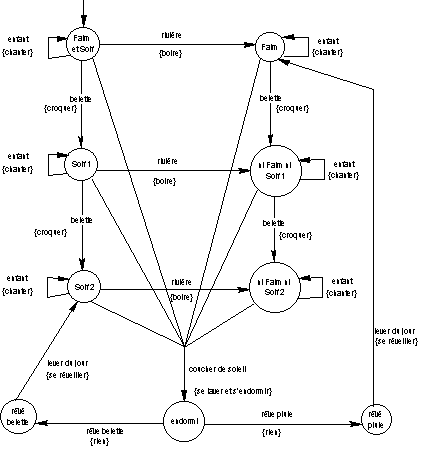
Le Kidor-Dyn est un animal fabuleux que peu d’entre nous ont eu le loisir de croiser sur leur chemin... À sa naissance (vers 7h00 du matin), le Kidor-Dyn a faim et soif. Lorsqu’il passe près d’une rivière, il boit, et cela lui suffit pour la journée. Lorsqu’il croise une belette, il la croque, et cela lui suffit pour la journée. Il peut cependant, au hasard des rencontres, croquer une seconde belette mais jamais trois dans la même journée. Lorsque le soleil se couche, le Kidor-Dyn fait sa toilette et s’endort, qu’il ait croisé ou pas de rivière ou de belette dans la journée... Le lendemain, il a à nouveau faim et soif, à moins qu’il n’ait rêvé, au cours de la nuit, de pluie (auquel cas il n’a pas soif) ou de belette (auquel cas il n’a pas faim). Par ailleurs, chaque fois qu’un enfant passe à proximité de lui dans la journée, le Kidor-Dyn chante une chanson...
¨Modéliser la vie trépidante du Kidor-Dyn à l’aide d’un automate avec actions.
Nous commençons par énumérer les événements et les actions… Les états sont alors nécessités par le fait que notre « animal » peut avoir des réactions distinctes aux événements…
événements : rivière, belette, enfant, coucher du soleil, lever du jour, rêve pluie, rêve belette.
actions : boire, croquer, chanter, se laver et s’endormir, se réveiller, rien (lorsque l’événement « rêve » survient, on subit l’événement…).
états : faim et soif, faim, soif 1, soif 2, ni faim ni soif 1, ni faim ni soif 2, endormi, rêvé belette, rêvé pluie.
Comme pour l’Exercice du téléphone, il faut mémoriser les différents états de « réveil », selon le rêve effectué, afin de se retrouver dans le bon état au lever du jour… Par ailleurs, il est nécessaire de « compter » les belettes, c’est-à-dire de distinguer les états où l’on a croqué une belette des états où l’on en a croqué deux…
L’automate correspondant est alors le suivant :