Bordeaux, mars 2002
| 6. Graphes : problèmes divers |
| Eric Sopena, Professeur au département Informatique
de l'IUT Bordeaux 1 Bordeaux, mars 2002 |
6.1 Arbres, arbres couvrants
Combien d’arbres différents existe-t-il avec 5 sommets ? avec 6 sommets ? avec 7 sommets ?
|
L’arbre ci-contre code un « dictionnaire » composé des cinq mots ABAT, ABIME, ACTE, ACTUEL et SOUTE. ¨On souhaite inclure dans ce dictionnaire le mot SORT. Que devient l’arbre ? ¨On souhaite maintenant inclure le mot SOU. Or, le mot SOUTE étant déjà présent, le mot SOU est « déjà construit » dans cet arbre… Comment distinguer alors le mot SOU du mot ABI qui, lui, n’appartient pas au dictionnaire ? Expliquez comment, à l’aide d’un tel arbre, il est possible de déterminer si un mot donné appartient ou non au dictionnaire. |
|
|
Le schéma ci-contre représente la carte d’un groupe de villages. Les sommets sont des villages et les arêtes des chemins reliant les villages. Pour chaque village, la valeur du sommet correspond au nombre d’enfants du village en âge d’être scolarisé. Pour chaque chemin reliant deux villages, la valeur correspond au nombre de rivières que doivent traverser à la nage les piétons empruntant ce chemin. |
|
On souhaite choisir l’un de ces villages pour y construire une école. Le critère de choix principal est la sécurité : on veut minimiser le nombre de traversées à la nage !…
Dans quel village doit-on construire cette école ?
|
Combien d’arbre couvrants différents les graphes ci-contre possèdent-ils ? |
|
6.2 Graphes hamiltoniens
Un groupe de 9 élèves se réunit chaque jour autour d’une table ronde.
Combien de jours peuvent-ils se réunir si l’on souhaite que personne n’ait deux
fois le même voisin ?
Même question avec 10 élèves, élèves, n élèves…
Toujours avec 9 élèves, mais cette fois avec 2 tables, l’une de 4 places, l’autre
de 5… Avec trois tables de 3 places ?…
Cette fois, ces réunions quotidiennes concernent un groupe de 12 élèves, 6 filles et 6 garçons. On souhaite toujours que personne n’ait deux fois le même voisin, mais, cette fois, on souhaite également que chaque fille soit entourée de deux garçons… Combien de jours peuvent-ils se réunir ?
|
Est-il possible de parcourir le graphe ci-contre : |
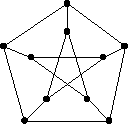 |
|
Un groupe de huit personnes se retrouve pour dîner. Le graphe ci-contre précise les « incompatibilités d’humeur » entre les personnes de ce groupe (une arête reliant deux personnes indique que celles-ci s’entendent très modérément…). ¨Proposez un plan de table (la table est ronde) pour ce groupe en évitant de placer côte à côte deux personnes « incompatibles ». Combien y a-t-il de solutions possibles ? |
|
| Fin des exercices sur les graphes |
6.1 Arbres, arbres couvrants
Combien d’arbres différents existe-t-il avec 5 sommets ? avec 6 sommets ? avec 7 sommets ?
Il est possible de classer ces différents arbres selon le nombre de feuilles (sommets sans fils) par exemple. Une façon de procéder peut-être plus « visuelle » consiste à les classer selon la longueur du plus long chemin dans l’arbre (on cherche ensuite à rajouter les « sommets manquants », sans les raccrocher aux extrémités du chemin pour ne pas le rallonger…). Nous obtenons ainsi :
¨ 3 arbres à 5 sommets :
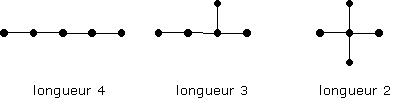
¨ 6 arbres à 6 sommets :
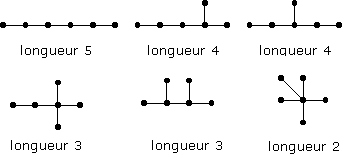
¨ 11 arbres à 7 sommets :
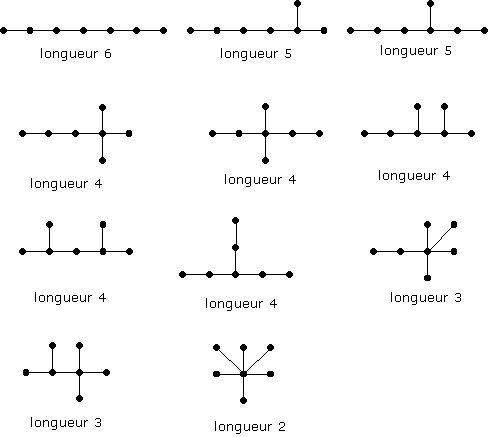
|
L’arbre ci-contre code un « dictionnaire » composé des cinq mots ABAT, ABIME, ACTE, ACTUEL et SOUTE. ¨On souhaite inclure dans ce dictionnaire le mot SORT. Que devient l’arbre ? ¨On souhaite maintenant inclure le mot SOU. Or, le mot SOUTE étant déjà présent, le mot SOU est « déjà construit » dans cet arbre… Comment distinguer alors le mot SOU du mot ABI qui, lui, n’appartient pas au dictionnaire ? Expliquez comment, à l’aide d’un tel arbre, il est possible de déterminer si un mot donné appartient ou non au dictionnaire. |
|
Pour rajouter le mot SORT, il suffit de prolonger l’arbre à l’aide d’une nouvelle « branche » (voir figure (a)).
Le mot SOU est « déjà présent » dans l’arbre… simplement, il se termine sur un sommet interne de l’arbre, et non sur une feuille. Il est donc nécessaire de distinguer, parmi les sommets internes (non feuilles) de l’arbre, ceux qui correspondent à un mot du dictionnaire… Il suffit par exemple pour cela de « marquer » (ou colorier) ces sommets à l’aide d’une marque particulière… Il est également possible (mais non nécessaire) de marquer les feuilles de l’arbre… (voir figure (b)).
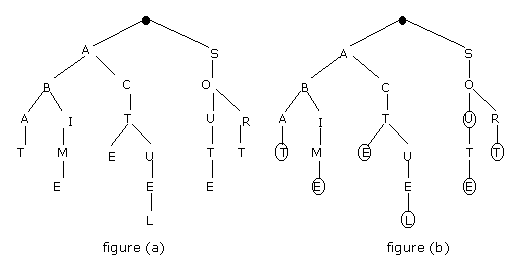
Pour rechercher un mot dans un tel arbre, il suffit de partir de la racine et de « chercher » les lettres du mot une à une. Lorsqu’on est sur un sommet et que l’on cherche une lettre, on parcourt les fils de ce sommet (les fils sont triés de gauche à droite par ordre alphabétique). Si la lettre n’est pas présente, le mot n’est pas dans le dictionnaire. Dans le cas contraire, on rejoint le fils trouvé et l’on passe à la lettre suivante… Si l’on trouve la dernière lettre du mot, et que le sommet correspondant est marqué, le mot est bien présent dans le dictionnaire.
|
Le schéma ci-contre représente la carte d’un groupe de villages. Les sommets sont des villages et les arêtes des chemins reliant les villages. Pour chaque village, la valeur du sommet correspond au nombre d’enfants du village en âge d’être scolarisé. Pour chaque chemin reliant deux villages, la valeur correspond au nombre de rivières que doivent traverser à la nage les piétons empruntant ce chemin. |
|
On souhaite choisir l’un de ces villages pour y construire une école. Le critère de choix principal est la sécurité : on veut minimiser le nombre de traversées à la nage !…
Dans quel village doit-on construire cette école ?
Il est possible, pour chacun des sommets du graphe, de calculer le nombre de traversées à la nage nécessaires si l’école est implantée dans le village correspondant… On obtient alors :
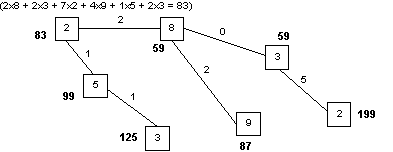
Nous avons ainsi le choix entre deux villages qui obtiennent le meilleur score (59)…
|
Combien d’arbre couvrants différents les graphes ci-contre possèdent-ils ? |
|
Il suffit de prendre le temps de les énumérer…
¨ nous obtenons 4 arbres couvrants pour le premier graphe :
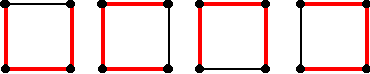
¨ 8 arbres couvrants pour le deuxième graphe :
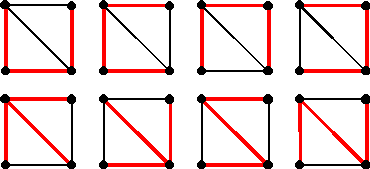
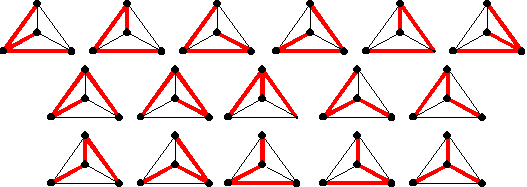
¨ et 16 arbres couvrants pour le troisième graphe :
6.2 Graphes hamiltoniens
Un groupe de 9 élèves se réunit chaque jour autour d’une table ronde.
Combien de jours peuvent-ils se réunir si l’on souhaite que personne n’ait deux
fois le même voisin ?
Même question avec 10 élèves, élèves, n élèves…
Toujours avec 9 élèves, mais cette fois avec 2 tables, l’une de 4 places, l’autre
de 5… Avec trois tables de 3 places ?…
Désignons par 1,2,…,9 les 9 personnes et considérons le graphe complet K9 à 9 sommets. Une composition de la table correspond à un cycle hamiltonien de K9 (un cycle passant une et une seule fois par chaque sommet). Si deux compositions de table correspondent à deux cycles ayant une arête commune, cela signifie que les deux personnes reliées par cette arête se retrouvent côte à côte… Ainsi, le problème revient à déterminer le nombre de cycles hamiltoniens disjoints de K9…
Le graphe K9 possédant 9 x 8 / 2 = 36 arêtes et chaque cycle utilisant 9 arêtes, ce nombre est au maximum égal à 4… Il vaut effectivement 4, comme le prouvent les 4 cycles hamiltoniens disjoints suivants :
1,2,3,9,4,8,5,7,6 — 1,3,4,2,5,9,6,8,7 — 1,4,5,3,6,1,7,9,8 — 1,5,6,4,7,2,8,1,9
Remarque. Ces cycles hamiltoniens ne sont pas obtenus « par hasard » (c’est également le cas pour la solution de l’
Exercice 10). En les observant attentivement, on peut remarquer qu’ils sont construits de la façon suivante :
premier cycle : 1,2,3,N,4,N-1,5,N-2,6,N-3,etc., où N représente le nombre total de sommets…
deuxième cycle : on conserve le « 1 » et on ajoute 1 aux autres éléments, avec la règle N+1 = 2.
chaque cycle est alors obtenu du précédent en conservant le « 1 » et en ajoutant 1 aux autres éléments (toujours avec la règle N+1=2…
Avec 10 élèves, nous avons 10 x 9 / 2 = 45 arêtes, soit 4 cycles hamiltoniens disjoints possibles (chaucn utilisant 10 arêtes). Avec 11 élèves, nous avons 11 x 10 / 2 = 55 arêtes, soit 5 cycles hamiltoniens disjoints possibles (chacun utilisant 11 arêtes). Dans les deux cas, il est possible de trouver les cycles correspondants :
pour 10 :
1,2,3,10,4,9,5,8,6,7 — 1,3,4,2,5,10,6,9,7,8 — 1,4,5,3,6,2,7,10,8,9 — 1,5,6,4,7,3,8,2,9,10
Lorsque N est pair, comme 10 ici, les arêtes restantes forment un couplage (elles sont non incidentes). En effet, il nous reste ici les arêtes 1-6, 2-10, 3-9, 4-8, 5-7 (voir également la solution de l’Exercice 10).
pour 11 :
1,2,3,11,4,10,5,9,6,8,7 — 1,3,4,2,5,11,6,10,7,9,8 — 1,4,5,3,6,2,7,11,8,10,9
1,5,6,4,7,3,8,2,9,11,10 — 1,6,7,5,8,4,9,3,10,2,11
En règle générale, k solutions sont possibles pour n = 2k+1 ou n = 2k+2 (plus un couplage pour n = 2k+2).
Revenons au cas des 9 personnes, cette fois avec une table de 4 places et une table de 5 places… Il s’agit toujours de décomposer le graphe complet en ensembles disjoints de 9 arêtes, mais cette fois, chaque ensemble doit correspondre à un cycle de 4 arêtes + un cycle de 5 arêtes. Avec trois tables de 3, chaque ensemble doit correspondre à trois tirangles…
Le nombre maximum de solutions discuté précédemment reste donc valable dans ces deux situations : nous aurons au plus 36 / 9 = 4 solutions… Là encore, on peut trouver 4 solutions :
une table de 4 et une table de 5 :
Je n’ai pas de solution « sous la main », mais je publierai la première
solution qui me parviendra… ;-)
trois tables de 3 :
(1,2,3)(4,5,6)(7,8,9) — (1,4,7)(2,5,8)(3,6,9) — (1,5,9)(2,6,7)(3,4,8) — (1,6,8)(2,4,9)(3,5,7)
Notons que pour chacune des situations de cet exercice, plusieurs solutions sont possibles…
Cette fois, ces réunions quotidiennes concernent un groupe de 12 élèves, 6 filles et 6 garçons. On souhaite toujours que personne n’ait deux fois le même voisin, mais, cette fois, on souhaite également que chaque fille soit entourée de deux garçons… Combien de jours peuvent-ils se réunir ?
L’idée de base est la même que pour l’exercice précédent, mais cette fois, du fait de l’alternance imposée fille / garçon, on raisonne sur le graphe biparti complet K6,6 (six filles et six garçons)… Ce graphe comprend 6 x 6 = 36 arêtes, et chaque cycle hamiltonien en nécessite 12. Il y a donc au maximum 3 solutions. En fait, trois solutions sont effectivement possibles (fi représente la i-ième fille, gi le i-ième garçon), par exemple :
( f1,g1,f2,g2,f3,g3,f4,g4,f5,g5,f6,g6) — (f1,g3,f2,g4,f3,g5,f4,g6,f5,g1,f6,g2)
—
(f1,g5,f2,g6,f3,g1,f4,g2,f5,g3,f6,g4)
|
Est-il possible de parcourir le graphe ci-contre : |
 |
Le graphe en question (connu sous le nom de graphe de Petersen) n’est pas hamiltonien. On peut par contre trouver un chemin hamiltonien, comme l’indique la figure ci-dessous.

|
Un groupe de huit personnes se retrouve pour dîner. Le graphe ci-contre précise les « incompatibilités d’humeur » entre les personnes de ce groupe (une arête reliant deux personnes indique que celles-ci s’entendent très modérément…). ¨Proposez un plan de table (la table est ronde) pour ce groupe en évitant de placer côte à côte deux personnes « incompatibles ». Combien y a-t-il de solutions possibles ? |
|
Il s’agit cette fois de trouver des cycles hamiltoniens dans le complémentaire du graphe. En voici un : B,C,H,A,F,G,E,D.
Que dire du nombre total de solutions ? il suffit de prendre le temps de les énumérer (ce que je n’ai pas encore fait ;-)…