 ,
Culture
,
CultureMichel Bénassy - Collège d'Albret - Dax
n°14, mars 2001
| La duplication du cube |
| |
 ,
Culture ,
CultureMichel Bénassy - Collège d'Albret - Dax n°14, mars 2001 |
Quadrature du cercle, trisection de l'angle, duplication du cube », l'infernale trilogie responsable de nombreux tourments pour les géomètres grecs de l'époque classique, s'avéra au fil des âges, constituer comme on le sait, un extraordinaire terrain d'investigations et de découvertes.
Le contexte des mathématiques grecques du milieu du Ve siècle av. J.C. impose aux géomètres l'usage exclusif de la règle et du compas. Cette exigence, confirmée un siècle et demi plus tard dans les trois premiers postulats d'Euclide, condamne les tentatives orthodoxes (*). Les obstinés vont user de moyens détournés pour parvenir à leurs fins : dispositifs mécaniques, sections coniques, autres courbes.
La légende raconte que, pour enrayer une épidémie de peste qui décimait Athènes, demande fut faite aux géomètres de doubler le volume d'un autel cubique du temple d'Apollon sur l'île de Délos.
Par confort, nous trahirons l'esprit grec en nous autorisant l'emploi
des notations modernes et des nombres réels positifs, mesures des longueurs.
Il s'agit donc connaissant l'arête a
d'un cube, de déterminer x tel que 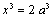 .Par bonheur Hippocrate de Chios
avait préalablement étudié cette question en montrant qu'il suffisait d'intercaler
« deux moyennes proportionnelles en proportion continue entre a
et 2 a », c'est
à dire de trouver x et y
tels que :
.Par bonheur Hippocrate de Chios
avait préalablement étudié cette question en montrant qu'il suffisait d'intercaler
« deux moyennes proportionnelles en proportion continue entre a
et 2 a », c'est
à dire de trouver x et y
tels que :
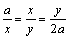 .
.
On a alors en effet : 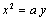 d'où
d'où 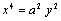 , or
, or 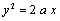 d'où
d'où 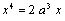 , or
, or 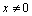 donc
donc 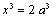 .
.
Munis de ce bagage, évoquons un système mécanique qui vise à fournir une solution géométrique au problème : la machine « de Platon ».
 |
Il est d'usage d'attribuer aux disciples de Platon l'idée de la conception de ce dispositif (on imagine mal en effet l'illustre philosophe revendiquer la paternité d'une invention s'écartant autant des « canons académiques ») : la machine, comparable à un pied à coulisse, se compose d'une équerre et d'une tige rectiligne qui coulisse perpendiculairement sur l'une des branches de l'équerre (fig. 1). Rappelons la propriété : si ABC
est un triangle rectangle en C et si H
est le pied de la hauteur issue de C alors Il s'agit d'« ajuster » habilement l'appareil
pour pouvoir considérer OA et OB
comme les termes extrêmes de la proportion d'Hippocrate (fig. 4) :
dans le triangle AEF
rectangle en E on a : |
Pappus d'Alexandrie (ive s. ap. J.C.) cite dans sa « Collection mathématique » plusieurs dispositifs visant à obtenir d'autres solutions « mécaniques » ; parmi ceux-ci figure le mésolabe d'Eratosthène.
Les savoirs mathématiques utiles ici : théorème de Pythagore, tangente d'un angle aigu ou triangles de même forme (machine de Platon), angles et parallélisme, théorème de Thalès (mésolabe) et calcul littéral élémentaire, appartiennent au registre du collégien de 3e ou du lycéen de 2de.
Les collègues intéressés pourront trouver sur le site Math du serveur académique des fichiers permettant une utilisation interactive de ces deux machines d'un autre temps.
(*) Dans un mémoire intitulé « Recherche sur les moyens de reconnaître si un problème de géométrie peut se résoudre par la règle et le compas » paru en 1837, le mathématicien français P-L. Wantzel montre que les questions de la duplication du cube et de la trisection de l'angle n'ont pas de solution à la règle et au compas et, en 1882, l'allemand C-L-F von Lindemann fait de même à propos de la quadrature du cercle.