Al-Khwârizmî (780-850), le « père de l’algèbre » est un savant de Bagdad, originaire du Khwârizm (comme son non l’indique), une région d’Asie Centrale.

Au carrefour de grands axes caravaniers et fluviaux, Bagdad est, au début du IX^e siècle, une plaque tournante du commerce international. Pesant déjà très lourd dans les domaines politiques et économiques, elle s’impose plus encore dans ceux de la science et de la culture. C’est à Bagdad que le processus de traduction des œuvres anciennes est, dès la fin du VIII^e, initié ; là aussi que sont écrits et publiés les premiers ouvrages scientifiques arabes. Le calife al-Ma’moun (813-833), en dynamisant la Maison de la Sagesse, fondée quelques années auparavant par son père Haroun al-Rashîd (786-809), donne l’impulsion décisive aux activités scientifiques et philosophiques. Le quotidien y est consacré à la traduction  et à l’étude de textes anciens, à la rédaction d’ouvrages nouveaux, à l’organisation de cours et de débats sur différents sujets (astronomiques, philosophiques, théologiques). Un facteur économique va aider au développement des activités intellectuelles : l’industrie du papier (dont la technique de fabrication aurait été empruntée aux Chinois). Beaucoup moins cher que le parchemin et le papyrus, le papier va favoriser la diffusion de la science dans l’immense Empire. Telle est donc en quelques mots la ville où travaille al-Khwârizmî.

L’acte de naissance officiel de l’Algèbre est la publication de son livre, dédié au calife al-Ma’moun. Voici en quels termes l’auteur y présente son contenu : « [c’est un abrégé] englobant les plus fines et les plus nobles opérations du calcul dont les hommes ont besoin pour la répartition de leurs héritages et de leurs donations, pour leurs partages et pour leurs jugements, pour leurs transactions commerciales et pour toutes les opérations qu’ils ont entre eux et qui sont relatives à l’arpentage, à la répartition des eaux de rivières, à l’architecture ainsi qu’à d’autres aspects ».

La première partie du livre se divise en plusieurs chapitres. Dans le premier, sont définis les objets de l’algèbre : les nombres (entiers et rationnels positifs), l’inconnue (Jidhr = racine) et son carré (Mâl = bien). Puis, il donne les six équations canoniques de degré inférieur ou égal à 2, en les accompagnant d’exemples. Dans le second chapitre, il fournit pour chacune des six équations son algorithme de résolution puis il expose les justifications géométriques de l’existence des solutions (voir : les 6 équations canoniques et leur résolution dans le cahier courts métrages).

Dans le troisième chapitre, al-Khwarizmî explique le procédé « d’algébrisation » d’un problème donné afin de le ramener à l’une des équations canoniques. Dans le quatrième, il expose l’extension des opérations arithmétiques classiques aux objets de l’algèbre (nombres positifs, monômes, binômes, trinômes) en tentant, parfois sans succès, de justifier géométriquement certaines de ces opérations. Le dernier chapitre est constitué d’une quarantaine de problèmes d’application.

La seconde partie du livre est consacrée à la résolution de problèmes de transactions commerciales, d’arpentage et de répartition des héritages. (exemple à la fin de ce document).

La nouveauté du livre est le fait qu’al-Khwârizmî ait rassemblé, pour la première fois dans un même ouvrage, un ensemble d’éléments (définitions, opérations, algorithmes, démonstrations) qui étaient soit éparpillés et sans liens entre eux, soit non formulés explicitement et indépendamment des problèmes d’application. C’est cette formalisation qui fera que l’apport d’al-Khwârizmî dans ce livre ait été considéré comme l’avènement d’une discipline.

Quelles sont les sources du livre ? Lorsqu’il s’agit de géométrie, d’arithmétique ou d’astronomie, les bibliographes arabes n’hésitent pas à nous fournir des détails sur les ouvrages fondamentaux, essentiellement grecs et indiens, qui ont nourri leurs premières recherches . Pour l’algèbre, c’est le silence. Les chercheurs sont donc réduits à interroger les textes eux-même en comparant leurs contenus à celui des documents babyloniens, grecs et indiens qui étaient susceptibles de constituer les sources de l’algèbre arabe. La première hypothèse est favorable à une origine grecque. Elle a été défendue au XIX^e siècle mais elle s’est avérée très fragile. En effet, les deux seuls ouvrages grecs qui étaient susceptibles d’inspirer les premiers algébristes arabes sont les Eléments d’Euclide et les Arithmétiques de Diophante. Or, le second ouvrage qui contient en particulier l’algorithme de résolution de certaines formes de l’équation du second degré, ne sera traduit en arabe qu’à la fin du IX^e siècle, c’est à dire presque cinquante ans après la mort d’al-Khwârizmî. Quant aux Eléments d’Euclide, la nature et la formulation de ses propositions sont géométriques et on ne peut y lire des problèmes d’algèbre qu’après avoir été sensibilisé au contenu de l’algèbre « rhétorique » telle que commençaient à la pratiquer les scientifiques arabes. A cela, il faudrait ajouter le silence d’al-Khwarizmî à propos des sources grecques alors que, dans ses écrits astronomiques et dans son manuel de calcul, il n’hésite pas à se référer aux sources indiennes. Ce dernier élément rendrait plus vraisemblable une éventuelle influence indienne surtout lorsque l’on sait que dès la fin du VIII^e siècle une mission de l’Inde, envoyée à la cour du calife al-Mansour (754-775), avait mis à la disposition des savants de Bagdad un Siddhanta, ouvrage astronomique renfermant un chapitre sur les procédés de calcul nécessaires à la résolution de problèmes astronomiques. Mais, cette influence indienne, si elle se confirmait un jour, n’a pu se réaliser qu’à travers une « adaptation » persane qui a peut-être eu lieu au VIIe siècle, ou à travers un « mixage » avec les procédés de résolution locaux hérités de la grande tradition babylonienne. Il est en effet probable que, durant la période de maturation qui a précédé l’avènement des savants du IX^e siècle, l’une des premières activités a été précisément la collecte, l’assimilation et l’enseignement des procédés algébriques anciens qui circulaient, à travers une transmission orale, dans les milieux des arpenteurs, des spécialistes des héritages et des marchands.

Après la publication du livre d’al-Khwârizmî, des auteurs vont se pencher de près sur son contenu et ils l’ont amplement commenté mais aucun de ces commentaires du IXe siècle n’a, à ce jour, été retrouvé. A côté de ces ouvrages perdus, on note la production d’autres écrits dont la caractéristique commune a été de réaliser l’interpénétration entre l’algèbre arabe et la géométrie grecque. L’Europe, elle, mettra cinq siècles (du XII^e à la fin du XVI^e siècle) à s’informer, étudier, assimiler et pratiquer cette nouvelle discipline, avant de se connaître une véritable explosion de créativité au XVII^e.

Énoncé

Un homme meurt et laisse un héritage m, à partager entre ses 3 fils ; il fait en outre une donation égale à ce qui reste de la part d’un des fils après avoir ôté le tiers de ce qui reste du tiers de l’héritage après qu’on lui ait retranché la part de l’un des fils.
Comment s’effectue le partage ?

Résolution

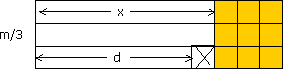
Si m est l’héritage, représenté par un rectangle, la part x de chacun des fils est représentée par un rectangle que l’on dissocie du tiers du grand rectangle. Il reste un rectangle, (correspondant à 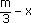) que l’on divise en trois carreaux. Chaque carreau vaut donc 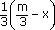. Si l’on retranche un carreau de la part d’un des fils (par exemple celle correspondant au rectangle inférieur, on obtiendra la donation, soit . 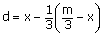La valeur de x correspond donc à 10 carreaux.