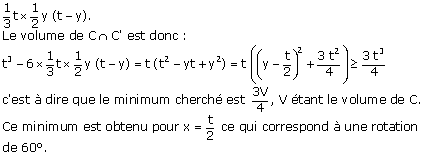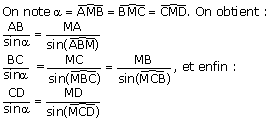
| Olympiades académiques de mathématiques 2001 Solutions |
| Antenne communication Bordeaux, juin 2001 |
Exercice I
1) La somme minimale est obtenue par :
1 + (2 + 1) + (2 + 1) + … + (2 + 1) + 2
avec 1000 termes entre parenthèses, donc
smin = 1 + 3 ´ 1000 + 2
= 3003.
La somme maximale est obtenue par :
1 + (4 + 3) + (4 + 3) + … + (4 + 3) + 4
avec 1000 termes entre parenthèses, donc
smax = 1 + 7 ´ 1000 + 4
= 7005.
2) On peut obtenir tous les entiers entre 3003 et 7005, de la manière suivante :
1 + 2 + 1 + 2 + 1 + 2 + …….. + 1 + 2
puis
1 + 3 + 1 + 2 + 1 + 2 + …….. + 1 + 2
puis
1 + 3 + 1 + 3 + 1 + 2 + …….. + 1 + 2
etc., jusqu’à obtenir
1 + 3 + 1 + 3 + 1 + 3 + …….. + 1 + 3.
Ensuite, on recommence en transformant progressivement les 3 en
4.
Ceci fait, on change progressivement les 1 en 2, et enfin on change progressivement
les 2 en 3.
Exercice II
On utilise la formule des sinus dans les triangles MAB, MBC et MCD. On note :
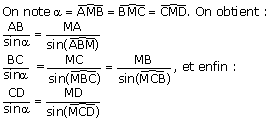
En remarquant que les angles

sont supplémentaires, donc ont le même sinus, on obtient deux relations :
MC = 2 MA et 2 MD = d MB.
L’ensemble des points M qui vérifient MC = 2 MA est le cercle de diamètre [BB’] où B’ est la barycentre des points pondérés (A ; 2) et (C ; -1) (symétrique de C par rapport à A).
L’ensemble des points M qui vérifient 2 MD = d MB est le cercle de diamètre [CC’] où C’ est le barycentre des points pondérés (B ; d) et (D ; -2) , sauf dans le cas où d = 2, car alors l’ensemble est la médiatrice de [BD] ;
M est donc à l’intersection de deux cercles.
Le cas limite est d = 6.
Si d<6, l’intersection est vide.
Si d = 6, les deux cercles sont tangents
en B’.
Si d >6, il y a deux points symétriques par rapport à la droite (AB). On
peut n’en retenir qu’un, si on considère que le terrain de jeu est un demi plan
limité par la droite (AB).
Remarque
On peut considérer que l’ensemble cherché contient aussi tous les points de
la droite (AD) privée du segment [AD] (cas où a = 0).
Exercice III
Soit x le gain du premier , y celui du second, z celui du troisième (0 < z < y < x) et N le nombre de parties.
N(x + y + z) = 20 + 10 + 9 = 39 donc (N = 1 et x + y + z = 39) ou (N = 3 et x + y + z = 13).
Pour N = 1, x = 20 , y = 10 et z = 9.
Pour N = 3 , on cherche
3 entiers rangés dans l’ordre croissant, de somme 13 et distincts 2 à 2 .
1, 2, 10 ; 1, 3, 8 ; 1, 4, 8 ; 1, 5, 7 ; 2, 3, 8 ;
2, 4, 7 ; 2, 5, 6 ; 3, 4, 6 .
Avec 1, 2 et 3 impossible de trouver une somme égale à 20 idem avec 1, 3, 8 ;
1, 5, 7 ; 2,3 , 8 ; 2, 4, 7 ; 2, 5, 6 et 3, 4, 6 .
La seule solution est x = 8, y = 4 et z = 1.
Exercice IV
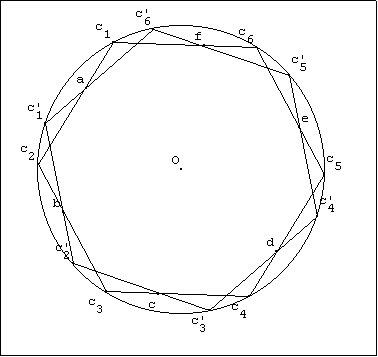
Désignons les six sommets du cube C, autres que A et B, par les numéros 1, 2, 3, 4, 5, 6. De même, désignons les six sommets du cube C’, autres que A et B, par 1’, 2’, 3’, 4’, 5’, 6’. Ces deux cubes ont la même diagonale donc le même volume.
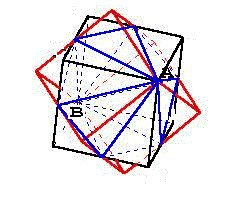
Le cube C’ est obtenu à partir du cube C par rotation d’axe (AB). Si on projette la figure formée par C et C’ sur un plan perpendiculaire à (AB), on obtient deux hexagones réguliers de même centre O, point d’intersection du plan et de (AB).
Les segments [1,1’] et [2,6’] sont dans des plans parallèles au plan de projection et ont des projections qui sont des segments parallèles, donc ces deux segments sont parallèles.
Donc (1,2) et (1’,6’) sont deux droites coplanaires. Elles se coupent
en un point a.
De même, on obtient b, c, d, e, et f.
Les points a, b, c, d, e, et f partagent les arêtes du cube C auxquelles ils appartiennent dans le même rapport (cela est dû à la rotation qui transforme C en C’).
Soit t la longueur de l’arête de C (et de C’).
Posons y = a1 (longueur du segment joignant
a à 1).
Alors y = a1 =
b2 = c3 =
d4 = e5 =
f6.
On a alors t - y = a2 = b3 =
c4 = d5 =
e6 = f1.
Pour obtenir le volume de C Ç
C’, il faut retirer à C six tétraèdres isométriques de volume